Всем снова привет! Как вы уже не помните, я писал блог на тему обнаружения игрока в шутере Return To Castle Wolfenstein, соответственно, в этот раз данный блог дополняет предыдущий блог. В этом блоге обсудим математическое моделирование стрельбы в шутерах с примером в программе Adobe After Effects
Перед ознакомлением с темой желательно вспомнить/ознакомиться со следующими темами в математике:
- Теорема Пифагора
- Тригонометрия
- Теория вероятности
- Уравнение прямой, проходящее через 2 заданные точки плоскости/пространства
На сколько нам известно, после обнаружения игрока, противники переходят в стадию атаки и начинают стрелять в игрока, но задумывались ли вы о том, откуда берётся траектория полёта снаряда?
Стоит обратить внимание, что обычно в играх пуля летит строго прямо, то ответ банально прост — пуля летит с помощью построенного уравнения прямой, которая имеет название — уравнение прямой, проходящее через 2 заданные точки плоскости/пространства, и сейчас мы это рассмотрим
Рассмотрим механику стрельбы на плоскости (2D игры)
Как нами было сказано раннее, уравнение прямой проходит через 2 точки. Возникает вопрос: Про какие точки идёт речь, которые необходимы для построения прямой через эти обе точки? Точки:
- Первая точка: Позиция стрелка имеющая координаты [x1, y1]
- Вторая точка: Позиция мишени (цели) имеющая координаты [x2, y2]
Важно отметить, что в роли стрелка и в роли мишени, могут быть как сам игрок, так и противник (пример NPC).
Вспоминаем каноническое уравнение прямой, которое имеет следующую формулу:
Данную формулу необходимо привести к общему уравнению прямой:
В параметр функции x подставляется значение пули/снаряда от старта до конца (до игрока, либо до другого препятствия).
Старт начинается от x1, y1, а заканчивается x2, y2. Временной промежуток полёта снаряда определяет разработчик. Пример временных промежутков:
- От секунды и меньше — это стрельба из автоматов, пистолетов и прочего огнестрельного в играх
- 2-3 секунды — это полёт снаряда из базуки, ракетницы и прочего долго летящего
Такт полёта снаряда определяется, как правило, счётчиком кадров в секунду. Если снаряд летит издалека, примерно полсекунды при 60 fps, то он совершит 30 тактов минимум до цели, а максимум это до тех пор, пока куда-то не попадёт (не обязательно попадать в цель, может быть промах)
Рассмотрим механику стрельбы на плоскости (2D игры) на примере в After Effects
Напомню, это больше годится для опытных пользователей After Effects, но постараюсь подробно описать, чтоб и новичок в данной программе смог реализовать пример полёта снаряда
Инструкция для реализации моделирования полёта снаряда:
- Создаём новый проект и в нём создаём новую композицию на 15 секунд
- Создаём первый объект, центрируем его якорную точку сочетанием клавиш Ctrl+Alt+Home и называем его Romaa712 (для x1, y1)
- Создаём второй объект, центрируем его якорную точку сочетанием клавиш Ctrl+Alt+Home и называем его Enemy (для x2, y2)
- Создаём маленький объект (который будет снарядом), лучше взять текстовый объект и назвать его «*» (звёздочкой одним символом), только после этого центровать его якорную точку сочетанием клавиш Ctrl+Alt+Home
koef = 470;
circleKoef = 450;
koefSin = -1.114;
PosRoma = thisComp.layer("Romaa712").transform.position;
PosEnemy = thisComp.layer("Enemy").transform.position;
Xmin = thisComp.layer("Romaa712").transform.position[0];
Xmax = thisComp.layer("Enemy").transform.position[0];
x=time*koef+Xmin;
if(x>=Xmax) { x=Xmax;}
y=((x-PosRoma[0])*(PosEnemy[1]-PosRoma[1]))/(PosEnemy[0]-PosRoma[0])+PosRoma[1];
t = Math.sin(time*koefSin)*circleKoef;
t=0;
if(x>=Xmax) { t=0;}
[x,y+t]
- Копируем код выше
- Идём в свойства слоя «*" (в анг. — Layer), в свойствах выбираем transform, затем выбираем position. На position нажимаем ПКМ (правой кнопкой мыши) и выбираем пункт Edit Expression и в него вставляем код выше.
- Результат, теперь перемещаем курсором мыши ползунок времени на timeline и смотрим, как прямо летит снаряд, к которому было подсчитано уравнение прямой, проходящее через 2 точки на плоскости. Также можно играться с перемещением объектов Romaa712 и Enemy
- ДОПОЛНИТЕЛЬНО! Идём в список эффектов и ищем Write-on. Данный эффект необходимо кинуть на слой " * " (в анг. — Layer). Brush Size выставляем 4 или 5, вместо 2, но потом на Brush Position нажимаем ПКМ (правой кнопкой мыши) и выбираем пункт Edit Expression и в него пишем transform.position, тогда кисть будет рисовать траекторию полёта снаряда. Потом перематываем на 5-ую секунду и смотрим полностью рисунок в виде траектории полёта.
Полёт гранат и подобных снарядов в 2D играх
Перед тем, как переходить к полёту снаряда в 3D играх (в пространстве) необходимо рассмотреть ещё полёт гранат на примере 2D игр и как это выглядит.
В первую очередь надо иметь понимание, что такой снаряд через всю карты кинуть невозможно, т.к. он не долетит до противника по причине маленького таймера (примерно до 5-ти секунд). Рассмотрим на примере противника (он же NPC), для которого сначала необходимо добраться как можно ближе к игроку и только при достижении определённого расстояния между ним и игроком он может кинуть в игрока гранату.
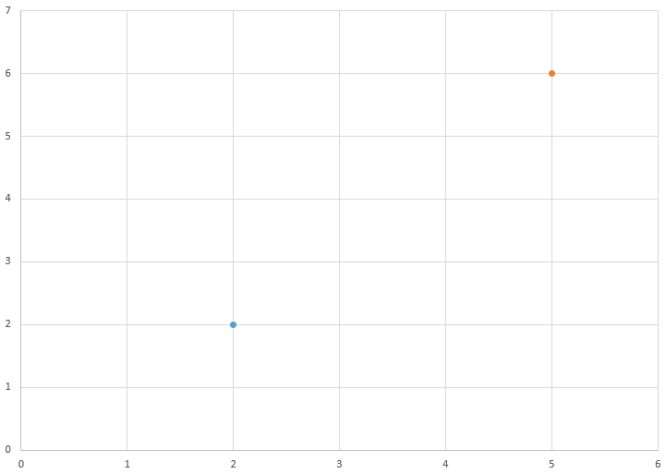
Реализация подсчёта дистанции NPC к игроку. Вспоминаем теорему Пифагора, где первым катетом является разница x(икс) позиции NPC и x(икс) позиции игрока, а вторым катетом является разница y(игрек) позиции NPC и y(игрек) позиции игрока.
Подсчитаем дистанцию между игроком и NPC. Координаты игрока это [2;2], а координаты NPC [5,6], а значит, что катет по разнице x-координат равен 3-ём, а катет по разнице y-координат равен 4-ём, соответственно, гипотенуза равняется 5-ти, т.к. это египетский треугольник. (см. рисунок ниже)
Первый шаг перед полётом гранаты выполнен - это подсчёт расстояния между NPC и игроком, а второй шаг - это траектория полёта гранаты.
Траектория полёта гранаты строется следующим способом:
- 1) Строим уравнения прямой, проходящее через 2 точки на плоскости между игроком и NPC.
- 2) по уравнению прямой строим промежуточные точки между двумя основными, например ещё 58 точек, что в сумме у нас будет 60 точек
- 3) У всех точек x(икс) будет точно такой же, который изменять не надо
- 4) у всех точек y(игрек) будет подсчитываться по следующему y = f(x)+sin(угол a)*k
- 5) 1-ая точка sin(180), 2-ая sin(177) и так до самого конца, где точка прилёта гранаты это точка игрока (тут sin(0) ), а точка вылета гранаты это точка NPC (как говорилось раннее это 1-ая точка, там же sin(180))
- 6) последнее это коэффициент k, если k=0 то граната летит строго прямо по траектории пули. Если k=1, то это как правило баллистика патрона (в том же pubg примерно так работает) Если k=3 и больше, то это уже ближе к реалистичному полёту гранаты
Для этого необходимо выполнить всю инструкцию для реализации моделирования полёта снаряда раннее, затем подправить код, убрав одну строку

В итоге код выглядит следующим образом:
koef = 470;
circleKoef = 450;
koefSin = -1.114;
PosRoma = thisComp.layer("Romaa712").transform.position;
PosEnemy = thisComp.layer("Enemy").transform.position;
Xmin = thisComp.layer("Romaa712").transform.position[0];
Xmax = thisComp.layer("Enemy").transform.position[0];
x=time*koef+Xmin;
if(x>=Xmax) { x=Xmax;}
y=((x-PosRoma[0])*(PosEnemy[1]-PosRoma[1]))/(PosEnemy[0]-PosRoma[0])+PosRoma[1];
t = Math.sin(time*koefSin)*circleKoef;
if(x>=Xmax) { t=0;}
[x,y+t]Разброс оружия в играх
Как нами было описано раннее, траектория стрельбы строго прямая и все снаряды летят в одну точку, соответственно, это не является реалистичным. Для добавления реализма к стрельбе необходимо обратиться к теории вероятности и тригонометрии.
Итак, под теорией вероятности подразумеваются случайные небольшие величины для случайной отдачи в момент стрельбы, а тригонометрия необходима для того, чтобы поле общего разброса имело круг форму, а не прямоугольную.
Для общего понимания, у нас отныне имеется окружность, центр которого является точкой из построенного уравнения прямой, а регулируется разброс изменением радиуса окружности, отмечается r.
Рассмотрим примеры значений радиуса в играх:
- r=0 в случае, если игрок целится из снайперской винтовки и стоит на месте
- r имеет максимально высокое значение в случае прыжка игрока или во время бега
- r имеет не большое значение, если игрок стреляет из пистолета/автомата
- r имеет определённое значение для использования дробовиков
- r имеет максимально высокое значение после первого выстрела без перерыва
Механика стрельбы в пространстве (в 3D играх)
Механика симуляции стрельбы в пространстве представляет из себя уравнение прямой, проходящее через две точки пространства строится точь в точь по той самой формуле, что и на плоскости, только в данный раз добавляется третья координата, которая отмечается как Z (пространство)
x1,y1,z1 - это точка стрелка
x2,y2,z2 - это точка цели
Данное уравнение считается через x(икс). В него подставляется значение в пределах [x1;x2], таким образом высчитывается параметр t, который затем используется в уравнениях с y(игрек) и z.
Данную механику наглядно можно лицезреть в Resident Evil 4 remake в миссии на вагонетках, когда в вас стреляют арбалетчики. Крайне наглядно летящая стрела из арбалета летит строго прямо, где x1,y1,z1 это координаты арбалетчика, а x2,y2,z2 координаты Леона и сразу стоит отметить, координаты у арбалетчика и Леона динамичные, и летящая стрела под это автоматически подстраивается.
Подводим итоги блога
В итоге после ознакомления с блогом у читателя появляется картинка о том, откуда берётся функция для полёта пули в играх, для полёта баллистического снаряда в играх и о том, почему необходим разброс после написания функции полёта пули.

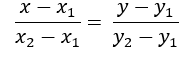
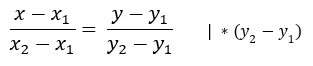
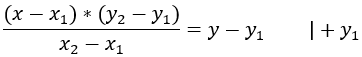
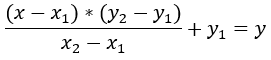
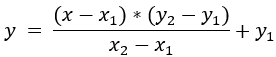
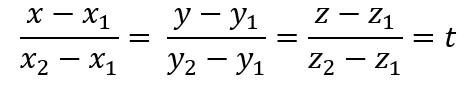








Лучшие комментарии
Когда ты — гуманитарий, подобные материалы и темы кажутся магией)
Предлагаю к ознакомлению
А почему? Если мы рассматриваем автоприцеливание на врага, то тогда подойдет уравнение прямой через две точки, но если мы рассматриваем свободное прицеливание, то тогда больше подойдет уравнение прямой с угловым коэффициентом. У тебя есть координата стрелка и есть угол линии прицеливания, и вот из этой координаты по этому углу и идет траектория выстрела, а попадание определяется принадлежит ли координата объекта траектории выстрела или нет.
Вопрос к автору он работает в геймдеве? Вообще обычно у каждого объекта есть вектор направление и каждый кадр ты прибавляешь к позиции вектор направления умноженный на скорость и дельту времени, можно добавить расчет ускорения, например что учитывать гравитацию. Так же можно через райкаст, мы просто кидаем через апи физики луч который находит столкновение и дополнительно показываем эффекты.
И не говори!)))
Автор статьи уверен/знает, что именно так и моделируется стрельба? А то у меня появилась парочка вопросов по блогу...
И вот тут возникает вопрос: а как именно определяется вторая точка (цель)? Допустим я стреляю в небо (не в противника), какую именно «цель» должна выбрать игра? И как именно она должна это делать? Этот же вопрос можно адресовать и для 2D игр, в которых отмечается не цель стрельбы, а лишь направление/угол (Worms, к примеру)
К слову, на примере Worms можно было бы и уточнить, как работает полёт гранат (когда игрок не строго отмечает цель, а лишь задает направление)
Спасибо за комментарий к моему блогу.
Тут у меня больше подразумевалась наводка именно от бота (NPC) на игрока, мол как её реализовать математическим моделированием
Спасибо за комментарий.
Моделирование стрельбы больше подразумевалось для NPC, мол как его запрограммировать стрелять в сторону игрока.
А если мы наводимся, то там считается чутка иначе: Прицеливание состоит двух точек в нашей модели (можно сказать вектором) — это центр нашей модели на уровне головы, а вторая точка это направление прицела, к которой применяются формулы тригонометрии для поворота.
Для наглядности, ниже продемонстрирована центральная проекция компьютерной графики, где первая точка про которую я говорил это центр проекции, а вторая точка это центр проекционной плоскости.
Спасибо за такой подробный комментарий со многими объяснениями. Если что, я не работаю в геймдеве.
Как я говорил раннее, я больше подразумевал направление снаряда от бота (NPC) в сторону игрока.
Так ведь у тебя в примере с помощью AE объект, который стреляет называется «Romaa712», что намекает на то, что стреляющий объект это ты, т.е. игрок, а не NPC.