В связи с выходом фильма Интерстеллар появилось сразу несколько блогов. В комментариях к одному из них я встретил непонимание основ теории относительности и вообще «математики пространств». Конечно же, я не могу оставить это просто так, поэтому включайте пространственное воображение и вспоминайте геометрию, будет немного сложно.
ТО — теория относительности
ОТО — общая теория относительности
ДПСК — декартова прямоугольная система координат
ОсновыДля начала хотелось бы заметить некоторую путаницу в терминах. Дело в том, что слово «пространство» используется сразу в двух смыслах — пространство реальное и пространство математическое. Что такое реальное пространство каждый из нас интуитивно представляет, а вот о математическом пространстве мы поговорим.
Понятие математического пространства возникает когда мы пытаемся описать положение тела в пространстве реальном. Есть много способов это сделать, но многие должны помнить из школы Декартову Систему Прямоугольных Координат (ДПСК), в ней вводятся взаимно-перпендикулярные оси, а положение объекта задаётся набором чисел — положением вдоль каждой оси. Если отбросить строгие математические формулировки, то все возможные значения координат объекта образуют математическое пространство.
Надо заметить, что пространства бывают разные. Например, можно задать пространство блогов, в котором каждый блог — точка этого пространства.
Свойства пространств
Как упоминалось, пространства бывают разные, но все они имеют некоторые свойства. Я не буду описывать все, но расскажу два важнейших и необходимых для дальнейшего изложения.
Размерность — минимальное количество параметров, необходимых для полного описания положения объекта в пространстве. Тут всё понятно, размерность пространства просто равна количеству координат объекта в нём.
Метрика. На этом надо остановиться поподробнее, так как именно метрика задаёт физические свойства реального пространства, которое описывает. Метрика пространства это формула, по которой рассчитывается расстояние от начала координат до точки в пространстве. Рассмотрим ранее упомянутую ДПСК. Из теоремы Пифагора следует, что данное расстояние есть
.
Выражение выше представляет собой метрику трёхмерного евклидового пространства.
Надеюсь, я смог дать представление о пространствах в математике и мы можем идти дальше.
Приложения в физикеОписанная выше математика имеет разнообразные приложения. ДПСК широко используется при описании нерелятивстских систем, то есть практически всего, что вы видите вокруг себя. Для ориентации на поверхности Земли используется сферическая система координат в которой координатами являются углы, отсюда и взялись градусы на карте.
В общей теории относительности данный математический аппарат расцветает во всей красе, элементы которой я постараюсь представить читателю.
Пространство в ТО. Для описания реального пространства нужно выбрать подходящую модель. Для этого заметим, что положение тела в нашем пространстве задаётся тремя координатами и временем, то есть оно четырёхмерно. С размерностью определились, теперь нужно задать метрику. Очевидно, что время отличается от трёх других размерностей — мы не можем двигаться по нему назад и менять свою скорость передвижения по нему, поэтому евклидова метрика нам не подходит, ведь в ней все размерности равноправны. Опущу причины для такого выбора, но подходящая метрика это
,где с — скорость света.
Пространство с такой метрикой называется пространством Минковского и оно псевдоевклидово. Видно, что теперь временная координата выделяется — она входит со знаком плюс, а пространственные со знаком минус. Из этого уравнения можно сделать много выводов относительно возможности передачи сигналов между двумя точками и даже получить преобразования Лоренца. Но вместо этого поговорим про кое-что более интересное.
Искривление пространства. Наверно, это самое «магическое» из того, что есть в ОТО. Искривление пространства — рабочая лошадка научной фантастики и надежда человечества на межзвёздные перелёты. Так как же это работает?
Чтобы приступить к изложению заметим, что если на тело не действуют никакие силы и оно обладает некоторой скоростью, то траектория движения тела — кратчайшая возможная кривая. В евклидовом пространстве это обычная прямая, на глобусе — дуга окружности, полученной сечением глобуса через его центр. В общем случае форма этой кривой задаётся метрикой пространства.
В ОТО для описания гравитации используется следующий механизм — тела, обладающие массой, энергией или импульсом изменяют свойства пространства, конкретнее его метрику. Если метрика пространства изменилась, то изменились и кратчайшие расстояния в нём. Поэтому объекты в пространстве меняют свои траектории так, чтобы они вновь стали кратчайшими. Нам же со стороны кажется, что на них подействовала какая-то сила — гравитация.
ВыводыКраткие итоги статьи. Реальное пространство можно описать с помощью математической модели, которая имеет определённые свойства. Важными свойствами являются размерность и метрика. В теории относительности используется пространство Минковского, а гравитация представляется как изменение его метрики или, что тоже самое, искривление.

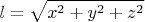










Лучшие комментарии
Где как, видимо.
Со школьной физикой непростая ситуация — очень сложно впихнуть в неё «высокие материи», поэтому надо либо придумать гениальный способ это сделать, либо не пытаться вообще.
Вузы надо рассматривать каждый в отдельности. Ведь, у них задача выполнить образовательный стандарт для направления подготовки и, по желанию, дать больше.
1) Школа — не лезь в розетку пальцами — убьёт.
2) Специальное техническое образование (ПТУ, но не экономическое, а слесари и иже с ними) — в розетку можно лезть пальцами, но сначала нужно обесточить.
3) Институт — для начала — в электрической цепи есть ток, он вырабатывается определённым образом, если сделать так — будет это, так — это, нужно вам всё, что я сказал выше, чтобы правильно направлять тех, кто будет пальцами лезть в розетку.
Ну или как-то так.
А затем ссылка на Гильбертово пространство. Вот они заблуждения.