Здравствуйте, Stopgameры! Вы когда-нибудь задумывались, почему арабские цифры выглядят так, а не как-то по-другому? Что стоит за их рисунком? Почему единица выглядит как «1», два как «2», три как 3 и т.д.? Почему именно так, а не иначе? Что это, прихоть художника выдумавшего их? Или всё гораздо сложнее и интереснее, в этом есть некое таинство?
Ещё в детстве, меня заинтересовало, зачем нас учат в школе писать 7 с чёрточкой по середине. Я спрашивал у учителей, они отвечали, чтобы не спутать единицу с семеркой. Звучит надуманно, поскольку на Западе уже давным-давно 7 пишут без черточки, так как её упразднили уже много лет назад. Тем не менее, они 1 с 7 уж точно никак не путают. Нет, тут что-то другое, более интересное и тайное, загадочное и древние. Ведь древние никогда ничего не делали просто так. У них во всём таится скрытый смысл, непонятный для широкой аудитории. Ведь знания раньше были засекречены, только малая часть населения, жрецы, владели ими. Так как, знание – это сила, а сила — это власть. Когда все наделены силой, власть исчезает, а вместе с этим исчезает и смысл жречества. Но время идёт, их знания постепенно просачиваются и распространяются.
В последнее время книжные прилавки наполнены различной литературой, пропагандирующие альтернативный взгляд на историю. Авторы этих книг полностью перечеркивают современное представление на древность. Их книги фантастичны, эпатажны и не признаны научным большинством. Факты, на которых построены повествования, косвенные, но зато этих фактов много и они остроумно дополняют друг друга, объясняя простые вещи простым языком. Несут ли они правду? Это уже вопрос веры. Только читатель может соглашаться с автором или нет.
В одной из этих книг, я нашёл ответ на свой детский вопрос, про семёрку. Книга называлась «Велес бог русов», автор Александр Белов. В ней я вычитал интересную теорию происхождения цифр. Она не признана научным большинством, поэтому считается не научной. Но, как и любая другая теория, другая точка зрения имеет право на жизнь.
Сейчас я процитирую вам её:
«До сих пор точно неизвестно кто именно изобрёл цифры. Про цифры говорят, что они арабские. Но что арабам считать в безводных пустынях Аравии и Сахары, где они вели кочевой образ жизни? Скот, поголовье скота. А что на голове скотинки красуется? Рога. Вот так и обозначали одну голову — одного быка галочкой — похожей на V. Галочка эта — рога — все, что осталось от бычьей головы. Как известно, в старину люди предпочитали рисовать картины-образы — пиктограммы. Затем эти картинки стилизовали, и они стали абстрактными значками, цифрами и буквами…. По сему от бычьей головы остались одни рога. Так вот: цифры — это и есть количество голов. Одна голова- два рога – галочка (V). Две головы — две галочки и т. л. В качестве экономии стали изображать одним росчерком пера количество голов. Ведь достаточно утомительно считать галочки, если их много. Так возникли цифры, где отражалось количество голов в стаде».
Рис. 1 является реконструкцией первых арабских цифр, иллюстрация взята из книги Александра Белова. Цифры 4,7 отличаются от современных записей достаточно сильно.
Цифровой ряд так называемых арабских цифр, где каждая цифра обозначает количество рогов. Цифра десять обнуляет числовой ряд, и он продолжается дальше на уровне десятков, сотен, тысяч и т. д. с участием все тех же первых десяти цифр. Количество рогов указано на цифрах.
Рис. 2 взят из википедии. Как можно заметить, цифра 4,6 больше похоже на современную запись, остальные любо совпадают с рис. 1, либо проигрывают им в плане логичности (соответствию со современной записью) рисунка.
Рис. 1 и 2 дополняют друг друга, но цифра 7 на них выглядит очень не привычно. Складывается мнение, что семёрка протерпела наибольшее изменение. Так ли это?
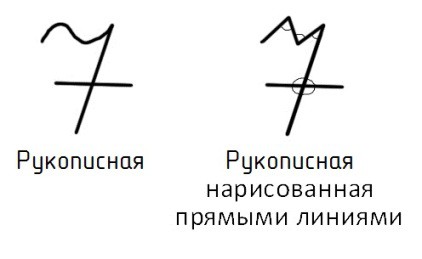
Давайте-ка разберёмся. Как уже говорилось ранее, 7 с чёрточкой посередине, уже много лет не пишется на Западе. В славянских государствах традиция такой записи ещё осталось. Возможно, осталось и ещё что-то? Давайте-ка попробуем записать рукописный символ семёрки. А затем, перерисуем ее, используя только прямые линии. И посчитаем количество рогов (элементов V).
Рис. 3, современная запись числа 7. Получилось ровно 7 «рогов».
Из этого следует вывод, что древняя запись арабских цифр, была близка к современной. С течением времени, для скорописи, прямые линии стали писать ровно и плавно. А некоторые элементы цифр упразднили за ненадобностью. Тем не менее, в ряде стран осталась древняя манера письма цифр, очень близкая к первоисточнику. Разве это не удивительно?
Но это ещё не конец нашего анализа.
Нам осталось рассмотреть ещё одну цифру, самую загадочную и необычную из всех – цифру ноль. Только это тавтология, так как само слово «цифра» происходит от арабского слова «сыфр» («ноль»).
Если мы рассмотрим ноль, то увидим круг, идеально ровный и плавный. Без начала и конца, в нём нет ни одного рога. Ничто, пустота, отсутствие поголовья скота. Но в то же время, ноль обозначал бесконечную малость. В рамках концепции рогов становиться понятным почему. В математике есть такой способ, разбиение большого на малое, на бесконечно малое. При таком подходе, можно из любой кривой линии сделать множество бесконечно малых прямых. Тоже самое можно провести и с кругом, символизирующим цифру ноль. Разбить его на элементарные отрезки, в результате мы получим бесконечно малое количество рогов.
В доказательство этого нарисуем круг. В него впишем квадрат. Впишем ещё один квадрат, только повернутый уже на 45 градусов. Затем скопируем эти 2 квадрата, и ещё раз впишем их в круг, повернув их таким образом, чтобы они делили пополам образующие дуги. Мы заметим, что внутри первоначального квадрата будет образовываться ещё одна окружность, в зависимости от количества вписанных квадратов она будет становиться плавнее. Сначала она представляла собой квадрат, затем многоугольник, затем ещё больший многоугольник, и так далее пока не станет казаться похожей на круг (обновите страницу и быстро суда переместитесь, что бы увидеть анимацию).
Выходит, что абсолютно круглых объектов нет. Любой круг состоит из прямых бесконечно малых линий. Бесконечность порождает в совокупности ничто. Так и наша вселенная в одной из многих теорий в совокупности имеет нулевую массу, энергию, плотность и много чего ещё нулевого.
0 – это вселенная, точка отсчёта, первичное начало. Сколь много смысла в одной цифре.
Так и науки, являются «квадратами», разных размеров: одни больше выяснили, другие меньше. Остюда и разные размеры. Общую картину мы сможем получить, взяв из каждой науки по квадрату одинакового размера, и провести операцию, что была описана выше. Образованная в центре сфера будет являть реальную не противоречивую картину мира. Но она будет являться лишь малой крохотной частью полной, абсолютной, бесконечно большой реальности.
Вот такая вот интересная теория происхождения цифр из рогов.
Статья была написана когда-то давным-давно, вашим покорным слугой, для сайта www.webstaratel.ru.


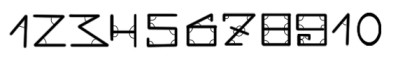











Лучшие комментарии
Процесс можно продолжать до достижения каждым отрезком бесконечно малой величины.
Справедливо, в силу несовершенства зрения и носителей информации.
С точки зрения человеческого восприятия — да. Но мне показалось, что в посте из этого утверждения следуют далеко идущие предположения.
Это оверкилл, достаточно вставить ссылку на картинку в пост ниже под изображением, кому надо, тот пройдет, чем тыкать обновление страницы и скакать в нужную и ее частей.
Таких цифр нет, есть: 0 1 2 3 4 5 6 7 8 9, 10 результат комбинирования. Правильнее все таки сказать число десять.
Солидарен с Ваней Лоевым, это просто не правильное утверждение, особенно, если переносить математическую модель в реальный мир. Будет время почитай про поверхностное натяжение и почему вода принимает сферообразную форму в вакууме.
Я бы его поменял на «на практике круг можно представить с помощью более простых геометрических предметов, манипулируя как количеством отображаемых предметов, так и скоростью их отображения», это как минимум будет честнее и не будет вводить людей в заблуждение.
Кстати на первой картинке у цифры 3 помечено всего 2 угла, 3тий видать забыли.
Мне лень залезать в гугл и проверять все эти теории, поверь — тут такие и без меня найдутся. Но в общем и целом топик мне понравился.
ЭТО ВИН!!!
Спасибо за подарок. :)
Здесь не переносится математическая модель, рассматривается только графическая часть. В реальной жизни всё состоит из молекул, атомов, кварков, преонов и прочего ещё неизведанного. Любой идеальный круг под микроскопом будет иметь шершавую поверхность. А под электронным — состоят из точечек, хотя эти точечки на самом деле не точечки и не круглые…