Это статья — текстовая версия вот этого видео:
Тот, кто сделал это видео и текстовую версию к нему — разные люди.
Если вам понравилась работа, просьба перейти по ссылке и поблагодарить автора лайком и комментарием с похвалой. Если что-то осталось непонятным, вы также можете задать вопрос либо в комментариях на Ютубе, либо здесь. Приятного чтения!
Введение
Последние 30 лет графика в игровой и киноиндустрии развивается довольно быстро. Ещё недавно персонажи в играх выглядели как бесформенная куча пикселей, а сейчас мы можем рассмотреть мельчайшие детали их образа: одежду, экипировку и прочее. В плане детализации виртуальных миров также удалось достичь ощутимых успехов. Всё это — заслуга огромного количества квалифицированных специалистов, которые постоянно изобретают новые подходы для улучшения качества картинки. Однако, недостаточно просто сделать красивую игру, нужно ещё добиться хорошей производительности на средних компьютерах и консолях. Чем выше качество картинки, тем более сложной становится задача.
Яркий пример тому — появление в играх технологии трассировки лучей, благодаря которой игры теперь выглядят ещё реалистичнее. Но с увеличением качества эффектов значительно выросла и нагрузка на видеокарты, что стало новым вызовом для разработчиков. Специалисты Nvidia понимали потенциальные проблемы внедрения новых технологий, поэтому заранее решили создать инструмент для их решения. Им стала технология DLSS, о которой мы сегодня и поговорим. В этом материале вы узнаете: что такое нейронные сети, как они обучаются и работают, а также об их возможностях при обработке изображений. Я постарался изложить всё как можно более доступно, не потеряв при этом в информативности. Наливайте чай, устраивайтесь поудобнее и давайте начинать!
Зачем пользователю высокое разрешение?
Прежде всего нужно разобраться в причинах появления алгоритмов повышения разрешения изображений. Большую роль в этом сыграл довольно агрессивный маркетинг производителей мониторов и телевизоров. Для экранов с большой диагональю важную роль играет количество пикселей на дюйм: чем больше, тем лучше. Многие считают, что для экрана с разрешением 1920×1080 диагональ не должна быть больше 27 дюймов, в противном случае отдельные пиксели будут сильно бросаться в глаза. Если же вы хотите монитор с большей диагональю, то добро пожаловать в мир Quad HD или 4К. Логично, что для телевизора с большой диагональю 4К разрешение выглядит очень даже уместно, поэтому, вероятно, и произошёл столь резкий скачок. Мы все хорошо помним, что разрешение Full HD появилось ещё в конце нулевых, а где-то с 2010-го года уже видеокарты среднего уровня вытягивали его с приемлемой производительностью. Следующей ступенью по логике должно было стать разрешение Quad HD. При нём количество пикселей на экране примерно в 1,7 раза больше, чем в Full HD. При 4К количество пикселей увеличивается уже в 4 раза, по сравнению с Full HD, поэтому нагрузка на видеокарту возрастает очень существенно. Производительность самих видеокарт становится больше с каждым годом, и многие ждут доступных вариантов, чтобы, наконец, шагнуть в мир высокого разрешения. Игровая индустрия также не стоит на месте. Количество полигонов 3D-моделей растёт постоянно, качество текстур тоже, что позволяет разглядеть мельчайшие детали на персонажах и окружении в целом. Для многих игр последних лет разрешения 1080р уже попросту начинает не хватать, а разрешения Quad HD или 4К постепенно перестают быть просто «хотелками». Об этом говорит рост продаж мониторов с разрешением 1440р для ПК и 4К телевизоров, которые преимущественно покупают владельцы консолей.
У многих тут возникает логичный вопрос:
«А что вообще даёт это самое повышенное разрешение? Мне и с Full HD монитором нормально живётся последние несколько лет. Смысл мне тратить деньги? Да и дорого это, ведь и видеокарту менять придётся»
Вот как раз с этим нам и нужно разобраться перед тем, как двигаться дальше.
При ежедневной работе за компьютером увеличенное разрешение банально даёт нам больше места для этих самых окон. Вот, например, сравнение рабочего пространства на мониторе 1080р и 1440р.
Как видите, на экране помещается значительно больше информации. А если поставить 4К, то рабочее пространство увеличивается ещё сильнее.
Однако, при таком разрешении текст и значки на экране становятся слишком мелкими, поэтому большинство людей использует масштабирование интерфейса, чтобы меньше напрягать глаза. Большое разрешение позволяет комфортнее работать с текстом, поскольку шрифты становятся более аккуратными и сглаженными за счёт большего количества сэмплов.
В играх же повышение разрешения даёт нам больше выборок при проецировании трёхмерной сцены на двухмерное изображение. Большее количество выборок, в свою очередь, позволяет уменьшить алиасинг, то есть эффект ступенчатости на изображении, и, вместе с этим, отобразить сверхмелкие детали текстур и объектов со сложной детализацией на большом расстоянии. Тут я говорю обо всяких заборах, проводах и растительности, поскольку именно на них чаще всего проявляется алиасинг и замыливание изображения при использовании сабпиксельных методов сглаживания. Вот почему использование повышенного разрешения сейчас является не роскошью, а вполне себе оправданным решением для повышения собственного комфорта.
Вот вам яркий пример из игры Quantum Break

На самом деле, в качестве примера вполне можно использовать практически любой современный проект, и разница будет очень даже заметна. Причина кроется в самом процессе выборки и закрашивания пикселей, который достаточно прост для понимания.
Поскольку границы всех объектов трёхмерной сцены представляют собой векторы, мы должны проверить пересечение этих векторов с центром каждого пикселя. Делать это можно разными методами: трассировкой лучей, или классической растеризацией. Останавливаться на этом мы сейчас не будем, ибо нам важен сам факт пересечения объекта с центром пикселя. По умолчанию производится одна выборка цвета для каждого пикселя, после которой он принимает 100% цвета нашего объекта. В этом, собственно, и заключается процесс сэмплирования.
Если спроецировать, например, треугольник, на изображение размером 5×5 пикселей, то мы получим вот такой результат.
Из-за маленького количества сэмплов на изображении мы видим нечто весьма
отдалённо напоминающее треугольник.
Если же мы проделаем тоже самое для изображения размером, например, 15×15, то получим гораздо более убедительный результат.
Конечно, если спроецировать это на сравнение Full HD и 4K, то разница будет не настолько серьёзная, но для большего понимания сегодняшней темы эти два изображения нам очень помогут. По сути, когда мы увеличиваем разрешение кадрового буфера в игре, мы именно это и делаем — увеличиваем количество выборок для проецирования.
Второй момент, который важен для понимания — это принцип работы множественной выборки, который лежит в основе большинства методов сглаживания. Если ранее для повышения качества картинки мы увеличивали параметр разрешения, то есть количество пикселей, то в плане сглаживания ситуация обстоит немного иначе. В одном из первых алгоритмов сглаживания — MSAA, количество пикселей остаётся неизменным, однако при этом увеличивается количество сэмплов, которые влияют на конечный цвет пикселя. При использовании двух выборок каждая будет влиять на цвет пикселя на 50%, при использовании четырёх выборок — на 25%, что напрямую влияет на производительность графического процессора. Именно за счёт добавления градаций в контрастных переходах между цветом объекта и фона и достигается нужный результат.
Тут стоит оговориться, что сейчас речь идёт именно о тех алгоритмах сглаживания, которые работают на этапе проецирования сцены на изображение, поскольку аналитические методы вроде TAA или SMAA работают совсем иначе. Тем не менее, суть работы данных методов и цель, для которой они предназначены, одни и те же — увеличить количество информации для определения конечного цвета пикселя на экране монитора. Думаю, теперь вам стало более понятно почему сглаживание требует так много ресурсов видеокарты. К ТАА, кстати, мы ещё вернёмся, когда будем подробнее говорить о реконструкции кадра игры, поскольку он имеет довольно много общего с технологией DLSS.
Знакомство с нейронными сетями
Аббревиатура DLSS расшифровывается как Deep Learning Super-Sampling — супер-сэмплирование на основе глубокого обучения. Для понимания первой составляющей этого определения мы рассмотрели две ключевые функции повышения качества изображения: увеличение количества выборок или супер-сэмплинг и сглаживание. Именно их и выполняет DLSS.
Теперь мы понимаем, почему разрешение — это довольно важная штука для повышения комфорта от просмотра картинки в современных проектах, но для рендера сцены при высоких значениях этого параметра требуется и большая производительность видеокарты. С ростом вычислительной мощности графических процессоров графика ведь проще не становится, а даже наоборот, следовательно, нужно искать новые подходы к повышению производительности, чтобы не жертвовать качеством изображения. Как оказалось, решение было найдено в области, долгое время остававшейся вне поля зрения широкой публики и ставшей массово известной лишь относительно недавно. Инженеры Nvidia из группы по изучению данных и машинному обучению предложили использовать нейронные сети, которые уже некоторое время активно применялись для восстановления повреждённых фотографий. Для решения такого рода задач на самом деле существуют и методы, которые не подразумевают использование нейронных сетей. Например, методы Телеа, Навье-Стокса или Криминиси, суть которых заключается в интерполяции значений цвета для заполнения недостающих данных.
Интерполяция — это процесс получения неизвестных промежуточных значений по набору уже известных. Например, для отрисовки плавного перехода между двумя цветами, так называемого градиента, как раз и используется линейная интерполяция. Каждый из вышеперечисленных методов имеет свои преимущества и недостатки, поскольку один может лучше работать с небольшими повреждёнными областями и плохо справляться с крупными, а другой — наоборот. Однако, в процессе изучения области нейронных сетей и попытках применения их для решения этих и не только задач, стало понятно, что именно они справляются с этой работой наиболее эффективно
Пример того, как нейронки удаляют шумы на фотографиях, позволяя рассмотреть на них мельчайшие детали
Изначально вычислительные машины были спроектированы для быстрого выполнения сложных расчётов и в этой отрасли они неимоверно хорошо себя показывали. Однако, с задачами классификации и синтеза компьютерам было работать крайне сложно. Алгоритмы для распознавания каких-либо объектов на изображении выглядели бы очень громоздко, представляя собой гигантский и неповоротливый кусок кода, который всё равно справлялся бы с такими задачами не очень эффективно. Мозг человека же с расчётами справляется не очень быстро, а вот распознавание образов и анализ внешней не всегда структурированной информации является нашей сильной стороной. Именно поэтому вопросами симуляции работы мозга в виде компьютерной модели и занимается огромное количество людей по всему миру.
Концепция нейронных сетей была описана Уорреном Мак-Каллоком и Уолтером Питтсом ещё в 1943-м году, однако первый алгоритм обучения был предложен только лишь в 1949 году Дональдом Хэббом. Несмотря на это, активное применение нейросетей началось относительно недавно, и причиной тому послужил рост вычислительной мощности центральных и графических процессоров, которые сейчас позволяют выполнять необходимые вычисления для обученных моделей в реальном времени. Оказалось, что нейросети — это очень гибкий инструмент, который по факту позволяет решать огромное множество задач от классификации образов и синтеза изображений до сложного регрессионного анализа, и вождения автомобилей.
Что же такое искусственная нейросеть?
Искусственная нейронная сеть — это математическая модель, функционирование и принцип организации которой напоминает биологические нейронные сети
Если мы посмотрим на то, как устроена биологическая нервная клетка — нейрон, то можно выделить несколько основных её составляющих: дендриты, тело, ядро и аксон. При образовании связи между двумя нейронами аксон одного нейрона присоединяется к телу, дендриту или аксону другого нейрона, а место их соединения называется синапсом.
Нервная система биологических существ состоит из миллиардов таких нейронов, а связи между ними устанавливаются в процессе их развития. Основная задача нервной системы — это получение информации из внешних источников и формирование шаблонов сигналов для передачи их по всей сети. Количество нервных клеток растёт с первых дней рождения ребёнка, но связи между ними отсутствуют. Чтобы эти связи установить, ребёнка постепенно обучают различным аспектам, помогающим нам выживать и существовать в окружающем мире. Изначально он учится распознавать образы, звуки, форму и цвет предметов, учится ходить, есть и анализировать то, что происходит вокруг, а дальше уже в школе и университете осваивает сложные научные дисциплины. Процесс обучения занимает тем больше времени, чем сложнее биологическое существо. У человека на это уходят многие годы.
Когда связи созданы, при получении визуального образа происходит активация множества связанных нейронов, которые ранее уже наблюдали похожий предмет.
Если мы посмотрим на эту картинку, с помощью зрения мы определяем форму предмета и его цвет. Наш мозг на основе ранее полученного опыта наблюдения подобных предметов производит его классификацию: круглый, зелёный, съедобный. Далее из полученных признаков мы определяем класс — это фрукт. Имея опыт поедания фруктов такого типа, мы безошибочно определяем, что это яблоко. Похожие процессы происходят и при взаимодействии с более сложными предметами, например, велосипедом. Когда мы садимся на него, мы уже знаем, как им управлять. На основе ранее полученного опыта мы держим равновесие и задаём направление и скорость движения. Чем больше опыт вождения велосипеда, тем меньше мы задумываемся о том, как ехать и больше думаем над тем, куда. Это является причиной того, что в процессе получения опыта в нервной системе активируется один и тот же набор нейронов, при этом связей требуется всё меньше и меньше с каждой поездкой. Именно процесс построения и оптимизации связей между нейронами и называется обучением. Всё наше взаимодействие с миром — это набор программ и алгоритмов, сгенерированный сложной биологической структурой, способной обучаться
Если рассмотреть подробнее искусственную нейронную сеть, мы увидим нечто похожее на биологическую нервную систему. Ну, по крайней мере, схематично. Я не берусь утверждать, что искусственная нейросеть работает точь-в-точь, как биологическая, но некоторые параллели провести вполне допустимо. Чаще всего нейронные сети обозначают в виде графа для большей наглядности
На нём мы можем увидеть, что каждый нейрон связан со многими другими, за счёт чего и осуществляется передача сигналов. Общую структуру нейронной сети составляют входной слой, на котором мы передаём данные для обработки; выходной — на котором получаем результат работы сети; и скрытые слои, количество и тип которых определяются исходя из сложности задачи.
Чтобы понимать принцип работы нейронной сети, нужно разобраться в том, что из себя представляют две составляющих этого определения: нейроны и, собственно, сеть как набор связей между ними. Для простоты понимания, давайте, пока, представим нейрон как некую сущность, которая хранит число от 0 до 1. Само число в данном случае будет являться «активацией нейрона». На входном слое число определяется сигналом, который подаётся сети для выполнения какой-то полезной работы. На скрытом или выходном слое число получается в результате вычислений в предыдущих слоях и функции, которая определена для конкретного нейрона в слое. Связи между нейронами называются «весами». Значения весов, по сути, означают «силу» каждой конкретной связи между нейронами; то, насколько она влияет на активацию нейрона. Согласно теории Дональда Хэбба, именно веса определяют то, насколько правильно будет работать обученная модель нейронной сети на наборах незнакомых данных, и именно правильный подбор этих значений является конечной целью всего обучения.
Говоря о машинном обучении, чаще всего подразумевают две его разновидности: «обучение с учителем» и «обучение без учителя». Первый подход подразумевает обучение сети на тренировочном наборе размеченных данных. По окончанию работы сеть сверяет полученный результат с правильным ответом и, если он неверен, выполняет корректирование настраиваемых значений.

Работа нейронной сети
Чтобы понять, как работает и обучается нейронная сеть, предлагаю разобрать довольно классический пример задачи по классификации — распознавание рукописных цифр. Давайте рассмотрим решение такого типа задач на примере этой нейронной сети с прямым распространением. С её помощью мы сможем разобраться что происходит внутри таких сетей. Прямое распространение или «Forward feeding» означает, что данные проходят от начала сети — с входного слоя — до её конца — выходного слоя. При этом модель не содержит замыканий или циклов, которые повторно проводят данные через отдельные нейроны. Чтобы эта модель смогла распознавать цифры, нужно сначала обучить её это делать.
Для этого нам потребуется специальная база данных Национального Института Стандартов и Технологий — MNIST, состоящая из 60000 образцов цифр, которые были размечены и приведены к определённому формату. Каждая цифра представлена в виде изображения в градациях серого с разрешением 28×28 пикселей, каждый из которых имеет значение яркости от 0 до 1. Это изображение подаётся на вход нейронной сети, состоящий из 784 нейронов, каждый из которых принимает значение яркости конкретного пикселя в картинке.
Тут важно уточнить, что картинка представляет собой двумерный массив, а первый слой нейронов — одномерный. Поэтому для передачи изображения необходимо выполнить его преобразование путём последовательного совмещения всех строк изображения в одну. Умножив 28 на 28 как раз и получается 784, поэтому количество нейронов входного слоя было выбрано не случайно. Десять нейронов выходного слоя регламентируют цифры от 0 до 9, а их активация также будет также определяться числом от 0 до 1. Значение активации нейрона показывает соответствие цифры на картинке конкретному варианту ответа. Точнее, насколько сеть уверена в том, что нечто на изображении, является, например, цифрой девять.
Также есть два скрытых слоя, состоящих из 16 нейронов каждый. Количество слоёв было выбрано автором этого ролика исходя из предположения о том, как в теории могла бы работать сеть и на какие этапы можно разделить задачу. Ну, а 16, по его словам, просто неплохо выглядит в качестве примера для обучения и может быть изменено в большую или меньшую сторону, если возникнет такая необходимость. Так или иначе, логика работы сети подразумевает, что активация определённых нейронов в каждом слое последовательно приводит к активации каких-то нейронов в следующих слоях, и так до тех пор, пока на выходном слоя не появится конкретный набор сигналов, который и даст нам вероятность определённого варианта ответа.
К примеру, передача на вход сети изображения 28×28 пикселей спровоцирует активацию конкретных нейронов на входном слое, которая приведёт к появлению конкретного шаблона активации нейронов в следующем слое, которое приведёт к появлению какого определённого шаблона в следующем, а оно, в свою очередь, приведёт к появлению шаблона на выходном слое и по итогу позволит сделать предположение о том, какая цифра находится на изображении.
Если мы посмотрим на схематичное изображение нейронной сети, у нас возникнет довольно логичный вопрос: «Почему эта структура даже в теории сможет решить какую-то задачу, тем более, такую нетривиальную? Почему она вообще способна делать что-то осмысленное?». Прежде всего, стоит понимать, что любую сложную задачу можно разбить на несколько простых, в результате решения которых мы приблизимся к получению требуемого результата. Обратив внимание на то, как выглядят цифры, мы можем увидеть, что каждая из них имеет какое-то уникальное сочетание составляющих элементов.
К примеру, цифра девять состоит из круга в верхней части и некой кривой линии снизу, восьмёрка состоит из сочетания двух кругов в верхней и нижней частях, а цифру четыре образуют одна горизонтальная и две вертикальные линии, и так далее. Теоретически, мы могли бы предположить, что первый слой сети выделяет из сочетаний пикселей отдельные линии — прямые или наклонные, а второй на основе полученных ранее данных определяет шаблоны, которые образуются отдельными линиями.
При нахождении какого-то конкретного шаблона или сочетания признаков нужные нейроны активируются, что в конце концов позволит сети выдвинуть предположение о том, какая именно цифра находится на изображении.
В данный момент мы не можем наверняка сказать, так ли на самом деле работает сеть, но давайте попробуем пока остановиться на этом, чтобы разобраться в процессе, а после вернёмся к этому вопросу, дабы подтвердить или опровергнуть нашу гипотезу. Тем более, что, рассматривая работу сети таким образом, можно представить и другие задачи, где такое распознавание могло бы пригодиться. Выделение определённых признаков может быть полезным при распознавании более сложных объектов на изображении или, например, для обработки голосовых записей, ведь слова состоят из слогов, которые в свою очередь состоят из букв и так далее. Как я уже сказал выше, основная цель всей сети получить некую систему, которая, в теории, сможет комбинировать наборы пикселей в линии, линии в шаблоны, а шаблоны в цифры, но для большего понимания того, как это вообще работает, давайте посмотрим, что происходит на примере одного из нейронов второго слоя.
Предположим, что его цель — определить, содержит ли картинка какую-то грань в указанной области. Для начала обратим внимание на значения весов, которые соединяют все нейроны входного слоя с нашим рассматриваемым нейроном. Затем возьмём все значения активации нейронов входного слоя и умножим их на соответствующие значения весов. Полученное выражение называется «взвешенной суммой».
Для наглядности запишем значения весов в виде изображения, где красные пиксели означают веса с отрицательными значениями, а зелёные — с положительными, яркость же будет определяться примерным значением самого веса.
Если мы установим значения всех пикселей, кроме указанной области в ноль, а пиксели в самой области проинициализируем положительными значениями, тогда для получения взвешенной суммы нужно будет просуммировать значения пикселей этой области со всеми значениями прошлого слоя. Чтобы определить, присутствует ли в этой области какая-то грань, логично будет добавить некоторое количество отрицательных весов для окружающих пикселей. В таком случае взвешенная сумма будет больше в тех случаях, когда средние пиксели ярче, а окружающие темнее. После вычисления взвешенной суммы может получиться довольно большое число, с которым будет не очень удобно работать, поэтому для правильной работы сети нам необходимо, чтобы значения укладывались в диапазон от 0 до 1. Чтобы это сделать, прибегнем к использованию специальной функции, называемой «функцией активации нейрона», задача которой — поместить полученное значение в указанный диапазон. В зависимости от того, какое значение нейрона требуется получить, используются разные функции активации. Среди наиболее известных выделяют ReLU, гиперболический тангенс и сигмоиду. Если не углубляться в математику, то смысл их использования заключается в том, чтобы получить конкретное поведение функции «y» на основе значения аргумента «x».
ReLU — это линейная функция, которая говорит о том, что при любом значении «х» — меньше нуля, «y» будет равен нулю. Гиперболический тангенс и сигмоида имеют довольно похожие графики и по факту они нужны в тех случаях, когда значение «x» может быть отрицательным, при этом функция «y» возрастает на значениях «x» близких к нулю. На практике функция ReLU показала себя лучше всего по причине меньших требований к производительности, поэтому в глубоком обучении она часто является наиболее предпочтительной. После применения функции сжатия к взвешенной сумме выражение будет выглядеть вот так:
Но что, если требуется, чтобы нейрон активировался не во всех случаях, когда взвешенная сумма больше 0, а, например, при значении суммы больше 10? В таком случае необходимо добавить к взвешенной сумме ещё одно число — «смещение», которое в данном примере будет равно -10. Таким образом, значения весов будут влиять на формирование шаблона пикселей в конкретном нейроне, а смещение — на то, насколько большой должна быть взвешенная сумма, чтобы нейрон стал активен.
Но мы рассмотрели всего лишь один нейрон из тех, что находятся во всей сети. Каждый из оставшихся нейронов также связан со всеми нейронами предыдущего слоя и имеет свой набор весов и сдвиг. Таким образом, нетрудно посчитать, что общее количество весов и смещений для всей сети составляет примерно 13000. Это те компоненты, которые могут быть настроены путём вычислений и корректирования их значений. Получается, что в итоге всё сводится лишь к этому самому процессу — поиску правильных значений весов и смещений для всей сети, чтобы она корректно выполняла поставленную задачу. Как вы уже, вероятно, догадались, это и называется «обучением» сети.
Матричные вычисления
Кстати, есть одна вещь, которую во всём этом объяснении мы так и не увидели — матрицы, поэтому давайте ещё ненадолго вернёмся к тому, как вычисляется значение активации одного нейрона.
Если бы мы попробовали использовать запись такого выражения для каждого нейрона в сети, получилось бы довольно громоздко и неудобно. К счастью, есть и другой способ представления — матричный, который при этом позволяет сохранить суть всех вычислений. Для начала объединим все активации слоя в столбец — вектор. Затем представим все веса в виде матрицы, каждая строка которой определяет значения весов всех нейронов предыдущего слоя с конкретным нейроном следующего. Получается, что взвешенная сумма всех активаций предыдущего слоя в соответствии с этими весами соотносится с одним из членов матричного произведения того, что находится слева. Также, вместо добавления сдвига к каждому из этих значений по отдельности можно добавить к выражению все значения сдвигов в виде вектора. Затем останется только поместить полученное выражение в функцию сжатия, что по факту эквивалентно применению функции к каждому члену по отдельности. Если мы дадим матрице весов, и этим векторам краткое обозначение, то получим довольно компактное и удобное визуальное представление перехода активации от одного слоя к другому.
Тут стоит обратить внимание на ещё одну вещь. Если присмотреться к математическим операциям в выражении, можно заметить некоторую интересную их последовательность, которую мы могли уже ранее встречать. А встречали мы её на презентации Nvidia, посвящённой архитектуре Turing и, в частности, блокам для выполнения матричных вычислений. Да, я сейчас говорю о ядрах Tensor — блоках, в которых представлена аппаратная реализация выражения D=A*B+C, и именно такая последовательность действий используется для вычислений в этой нейронной сети. Хоть матрицы здесь и выглядят немного иначе, не стоит забывать, что это вычисления лишь для одного слоя.
Кстати, название специализированных блоков для работы с матрицами было выбрано не случайно. Тензор — это название объекта линейной алгебры, который позволяет особым образом хранить информацию о векторах. Хорошее видео на эту тему снял Дэн Флейш, где он на простых примерах объясняет, что такое тензор. Ролик небольшой, да ещё и с русскими субтитрами, поэтому информацию будет довольно просто усвоить. Тем не менее, я постараюсь коротко объяснить основную его мысль.
Предположим, у нас есть произвольный вектор в декартовой системе координат (система с осями Х, Y и Z. прим. редактора). Каким образом можно сохранить точную информацию о нём, чтобы любой человек смог однозначно отобразить этот же вектор на основе сохранённых данных? Оказывается, его можно описать базовыми векторами единичной длины. К примеру, чтобы попасть из начальной точки этого вектора в конечную, потребуется 3 базовых Х-вектора, 4 базовых Y-вектора и 0 базовых Z-векторов, поскольку вектор отображён на плоскости. Это и будет представление нашего вектора, которое можно записать в виде строки или столбца.
Таким образом, вектор будет являться тензором первого ранга. Обычное число — скаляр, будет тензором нулевого ранга. Тензором второго ранга будет являться матрица, а тензор третьего ранга вообще будет представлять из себя куб. Он выглядит как набор матриц, стоящих друг за другом. Если вдруг вам интересно как выглядят тензоры выше третьего ранга, то вот.
Для быстрой работы с тензорами Nvidia сделала специализированные блоки, которые справляются с такими вычислениями более чем в 8 раз быстрее обычных CUDA-ядер. Ядра Tensor оперируют небольшими матрицами 4×4, поэтому для расчёта матриц большей размерности на уровне драйверов их делят на небольшие блоки и выполняют вычисления уже с ними. Вычисления в нейронных сетях выполняются как раз в виде матриц, поэтому ядра Tensor очень значительно ускоряют как работу обученных моделей, так и процесс обучения сетей.
Но вернёмся к тому, с чего мы начали — пониманию, что такое нейрон. Ранее я предложил представить его в виде некоторой сущности, которая хранит значение. Теперь, когда мы лучше понимаем происходящее, правильнее будет говорить о нейроне как о функции, которая принимает на вход все значения активаций нейронов предыдущего слоя и значения весов, а на выходе даёт нам число от 0 до 1. Более того, вся нейронная сеть также является функцией, которая принимает на вход 784 числа, а на выходе отдаёт 10.
Безусловно, довольно сложно представить себе функцию, оперирующую столь огромным количеством значений, которая при этом ещё и подразумевает их правильный подбор для выполнения какой-то полезной работы. Однако, если мы посмотрим на сложность задачи, очевидно, что вряд ли с ней справилось бы нечто лёгкое для понимания. Тем не менее, нам ещё предстоит углубиться в процесс обучения нейронной сети и именно об этом я предлагаю поговорить далее.
Обучение нейросетей
Процесс «обучения» представляет собой подбор правильных значений для всех весов и смещений в рассматриваемой нейросети. Ранее я уже упомянул о том, что для этой задачи нам требуется два больших набора данных: обучающая выборка и тренировочная, на которой выполняется тестирование работы обученной модели. Давайте теперь поговорим о том, для чего эти наборы нужны, и как вообще происходит обучение. Наша задача на данном этапе состоит в том, чтобы передать сети два набора данных: изображения с цифрами и метки с правильными ответами для них. С их помощью она будет корректировать веса и смещения для улучшения своей работы. Затем уже на тренировочном наборе без ответов она будет пытаться определять, какая именно цифра представлена на каждой картинке.
Как мы помним, в нашей рассматриваемой сети каждый нейрон связан со всеми нейронами в предыдущем слое, а веса, которые определяют его активацию, показывают силу этих связей, то есть насколько конкретный вес влияет на эту активацию. Смещение же показывает, насколько большой должна быть взвешенная сумма, чтобы нейрон стал активен. При первом запуске сети значения весов и смещений задаются случайными числами, чтобы не делать это вручную. Думаю, не нужно объяснять, почему в этом случае сеть будет выполнять совершенно случайные действия, и при попытке передать ей изображение тройки из обучающего набора на выходе мы получим полный бред. Чтобы понять, как улучшить результат, нужно определить функцию ошибки, которая будет говорить сети: «Плохо, ответ неверный!»
На изображении находится цифра три, поэтому активация всех нейронов, которые не отвечают за тройку, должна быть равна нулю. Но недостаточно просто указывать сети на её ошибку, нужно объяснить, как её исправить. Для начала необходимо вычислить квадрат разности между правильным значением и неправильным ответом сети в каждом нейроне и сложить результаты между собой для определения величины ошибки. На самом деле, квадрат разности — это лишь один из возможных алгоритмов, но он достаточно наглядный, потому как представление о квадрате разности у нас имеется ещё из школьной программы. При правильном ответе сети, величина ошибки достаточно мала, в обратном же случае её значение будет больше с увеличением отклонения работы сети от правильного результата. Далее нужно определить среднее значение ошибки на большом количестве примеров из обучающего набора, которое покажет, насколько сеть ошибается в вычислениях. Мы уже знаем, что вся нейронная сеть представляет собой функцию, принимающую на вход 784 значения. Результат её работы — это 10 значений выходного слоя, определяемые на основе весов и смещений, которые требуют правильного подбора значений на этапе обучения. Чтобы приступить к самому подбору, мы должны сначала определить, насколько нужно скорректировать эти параметры.
При передаче на вход необученной модели картинки с цифрой 2, например, мы получим полную ерунду вместо ответа. Сравнив полученный результат с ответом, мы можем увидеть, что для коррекции ошибки значение активации нейрона, отвечающего за цифру 2, нужно повысить, а остальные — понизить. Также в зависимости от величины отклонения от правильного ответа можно определить, какие значения нейронов важнее исправить в конкретном случае. Основываясь на этих данных, мы можем корректировать значения весов, соединяющих нейроны выходного слоя с предыдущим, после чего повторить операцию уже для связей между нейронами скрытых слоёв и так до тех пор, пока не достигнем входного слоя сети. Двигаясь от последнего слоя к первому, мы постепенно сможем скорректировать общую ошибку всей сети, поэтому такой подход и получил название «метод обратного распространения ошибки».
Теперь, когда у нас есть конкретный план действий, осталось разобраться, как происходит сам процесс подбора значений. Для этого нужно вернуться к тому, что такое функция ошибки и как она работает.
Как я и говорил ранее, сама нейронная сеть — это тоже функция, которая на основе входных данных и параметров в виде весов и смещений определяет значения на выходе. Функция ошибки, в свою очередь, принимает на вход 13000 значений весов и смещений, а на выходе выдаёт число, характеризующее величину ошибки работы сети. Поведение этой функции определяется в процессе работы с большим количеством обучающих примеров. Чтобы упростить понимание, давайте представим функцию не 13000 переменных, а всего одной. Если функция простая, то несложно будет найти на графике в какой точке её значение будет минимальным. Однако, для сложных функций это уже будет не так очевидно, поскольку она может иметь несколько локальных минимумов. Проверяя каждую из множества точек кривой, можно определить направление возрастания и убывания функции, чтобы найти локальный минимум.
Теперь рассмотрим более сложный пример,
для наглядности.
На плоскости отобразим область определения функции двух
переменных — Х и У, а функцию ошибки — как поверхность красного цвета над ней.
Возвышения на поверхности показывают направления максимального возрастания
функции, а впадины, соответственно, — направления её убывания. По аналогии с
прошлым примером, для каждой точки также нужно найти локальный минимум, то
есть, понять в каком направлении начать двигаться, чтобы оказаться в нижней
точке поверхности. Направление возрастания функции показывает вектор, который
называется «градиентом», а его длина указывает на то, насколько плавно или
резко эта функция возрастает. Логично, что отрицательное значение градиента в
таком случае покажет направление убывания функции и то, насколько быстро это
происходит. Алгоритм минимизации функции ошибки шаг за шагом вычисляет
отрицательный вектор-градиент для каждой точки, благодаря чему и определяется
минимум этой функции. Ровно то же самое выполняется и для функции 13 000
переменных. Этот процесс и называется «градиентным спуском». Если представить
все веса и смещения нейронной сети как один вектор-столбец, а отрицательный
градиент как второй вектор-столбец, то значения вектора-градиента показывают,
насколько нужно скорректировать значения первого столбца, чтобы приблизить их к
правильным. Именно благодаря алгоритму минимизации функции ошибки с каждым
примером из обучающей выборки сеть постепенно «обучается» получать верный
результат. В процессе обучения данные из обучающей выборки передают разбитыми
на группы по несколько штук, количество которых указывает пользователь перед
запуском. Это нужно для того, чтобы повысить эффективность и скорость процесса
обучения. Вместо того, чтобы обрабатывать несколько тысяч примеров в одном
проходе, через сеть последовательно прогоняют несколько небольших наборов, для
каждого из которых сначала определяется значение ошибки, а затем происходит её
минимизация. Если вновь взглянуть на визуальное представление этого процесса,
мы увидим, что сеть не сразу движется по оптимальной траектории к минимальному
значению функции, а делает это постепенно с каждым пакетом данных.
Такой подход называется «стохастическим градиентным спуском». В результате всех этих действий нейронная сеть постепенно скорректирует значения всех весов и смещений и научится работать уже с незнакомыми данными из тренировочной выборки.
Учитывая количество операций и вычислений, думаю, теперь понятно почему обучение нейронной сети требует очень мощного железа. Nvidia, к примеру, для обучения модели DLSS использует свои суперкомпьютеры DGX с огромной вычислительной мощностью. А вот работа обученной модели уже не требует столько ресурсов, ведь значения всех весов уже подобраны.

Как итог, при текущей архитектуре сеть распознаёт около 96% всех чисел. Более того, если немного поработать со структурой слоёв результат можно улучшить результат до 98%. А если пересмотреть архитектуру сети, то и того больше. Учитывая, что мы не сообщали сети что именно нужно искать на картинке, она справляется с задачей очень неплохо. Когда мы начали разбираться с обучением, я сказал, что мы ещё вернёмся к тому, как работает сеть. Изначально мы предположили, что один из скрытых слоёв может искать на изображении отдельные формы и линии, а второй — обобщать полученную информацию в шаблоны. На самом же деле, сеть работает совсем по-другому.
Ранее мы уже видели, как можно графически представить связи всех нейронов первого слоя со вторым. Но если мы посмотрим на изображения, полученные на каждом нейроне, мы увидим лишь случайные наборы пикселей.
В процессе обучения сеть подобрала оптимальные значения для всех весов и смещений, и именно эти значения мы и можем наблюдать здесь. Получается, что сеть умеет определять цифры, даже не понимая, как они выглядят. Убедиться в этом весьма нетрудно, достаточно лишь дать ей на вход картинку со случайными значениями пикселей. По идее, наблюдая подобное нечто, сеть не должна была активировать ни один нейрон, однако она уверенно выдаёт ответ в виде пятёрки. Связано это с ограничением при обучении, ведь изначально мы и не требовали от сети рисовать цифры.
Что ж, наше первоначальное предположение о том, что эта конкретная сеть ищет на изображении линии и шаблоны не оправдалась. Дело в том, что мы рассмотрели довольно базовую архитектуру сети — многослойный перцептрон, но понимая принципы его работы мы сможем разобраться с более совершенными моделями. На текущий момент различных архитектур нейросетей довольно много, но все их рассматривать мы, естественно, не будем. Нас интересуют конкретные типы, которые лежат в основе DLSS. Один из таких — это свёрточные нейронные сети, к которым я и предлагаю перейти.
Сверточные нейронные сети
Рассматривая первую модель нейронной сети, мы могли наблюдать некоторые неудобства при передаче изображения на её вход. Мы были вынуждены выполнять преобразование двумерного массива 28×28 пикселей в одномерный из 784 элементов. Но что, если наша картинка имеет на порядок большее разрешение? Скажем, 1920×1080. Для подобной картинки входной слой имел бы более двух миллионов нейронов, что достаточно неудобно. Да и, кроме того, на изображении может находиться не только какой-то простой объект типа цифры, но и нечто более сложное. А что, если объектов и вовсе несколько? Сложность сети с подобной архитектурой возросла бы значительно. Именно поэтому для работы с изображениями требовался совершенно иной подход, который позволил бы иначе подойти к анализу представленной информации. Он получил название «свёрточная нейронная сеть», идею которой предложил французский специалист по машинному обучению Ян Леку́н. Задача этой архитектуры состоит в сжатии информации на изображении с сохранением значимых данных. Это возможно благодаря специальным слоям «свёртки» и слоям сжатия.
Этап свёртки заключается в создании карт признаков изображения — «feature maps». Они получаются путём пропускания исходного изображения через ряд фильтров, каждый из которых подчёркивает нужную информацию. Каждый из фильтров представляет собой небольшую матрицу заданного размера, например, 3×3 пикселя, с различным набором чисел. Он называется «ядром свёртки». Благодаря тому, что эти наборы чисел отличны друг от друга, они позволяют генерировать уникальные карты признаков. Один фильтр позволяет выделить на изображении вертикальные линии, другой — горизонтальные, третий — диагональные и так далее. Такой результат получается в результате прохода ядра свёртки по всему изображению. Оно последовательно перемещается от верхнего угла к нижнему, тем самым генерируя новое изображение. После этого мы можем сжать его с помощью слоя, называемого «Max Pooling». Установив размер ядра 2×2 пикселя, мы также проходим им по картинке со слоя свёртки. Max Pooling выбирает из матрицы 2×2 максимальное значение и записывает его в один пиксель, тем самым уменьшая размер изображения в 4 раза. Если мы сравним результат с тем, что было на входе, то увидим, что вертикальные линии не только не пропали, но и стали более различимыми.
Слои свёртки и пулинга часто используются в паре, и таких пар в сети может быть несколько. Их количество зависит от того, насколько нужно сжать изображение и сколько карт признаков нужно получить. В некоторых сетях слой Pooling вообще не используется, поскольку после его применения часть информации с изображения теряется, поэтому его функции перекладывают на слой свёртки. Тем не менее, подход с пулингом всё ещё применяется во многих сетях, например, в тех, о которых ещё пойдёт речь, поэтому стоит понимать принцип работы этой операции.
Чтобы было более понятно, как работает свёрточная сеть, рассмотрим пример решения той же задачи с распознаванием цифр. Я нашёл отличный сайт с визуализацией, где мы можем посмотреть, что происходит на каждом из слоёв. Ссылка будет в источниках, если сами захотите посмотреть. На вход нейронной сети мы подаём изображение с цифрой 5, после чего слой свёртки проходит по нему набором фильтров, как я и описывал выше. Мы получили несколько карт признаков, на которых можно хорошо наблюдать результат работы фильтров. На одном изображении мы видим, как фильтр выделил нижнюю часть горизонтальных линий, на другом — верхнюю их часть.
На некоторых других картах подчёркнуты уже вертикальные и диагональные линии. С одного чёрно-белого изображения слой свёртки создал целых 6 карт признаков. Количество этих карт можно увеличить, в зависимости от сложности изображения и того, что вы хотите на нём обнаружить. При обработке цветных изображений, например, операцию свёртки проводят с каждым из цветовых каналов: красным, синим и зелёным, поэтому и карт признаков потребуется больше.
Далее слой Max Pooling уменьшает размерность карт признаков, созданных на втором слое. Здесь мы можем хорошо видеть, что несмотря на более низкое разрешение, основная информация на изображениях сохранилась и осталась читаемой. На четвёртом слое снова происходит свёртка ещё большим количеством фильтров, и на нём уже данные выглядят практически неразличимыми для человека. Следом ещё один слой Max Pooling снова уменьшает разрешение карт предыдущего слоя. А вот далее, чтобы нейронная сеть смогла выдать какой-то ответ, мы должны преобразовать полученные карты признаков в одномерный вектор. Для этого потребуется ещё один тип слоёв — выравнивающий. Он необходим для того, чтобы отправить данные на полносвязный слой. На этом этапе модель сети становится похожа на ту, что мы видели в первый раз. Выравнивающий слой соединяется с полносвязным слоем с меньшим количеством нейронов, после чего уже он соединяется с выходным слоем из 10 нейронов, где мы и получаем ответ. Благодаря отличной визуализации мы можем увидеть то, что происходит на скрытых слоях свёрточной сети. Это позволяет более точно представлять и понимать её работу. Как и в случае с первой сетью, все веса и смещения этой модели также подбираются в процессе обучения, никаких отличий в этом плане нет. Реальными примерами таких свёрточных нейронных сетей с классификацией являются модели компании Visual Geometry Group — VGG-16 и VGG-19, где номер соответствует количеству слоёв в сети. Архитектура VGG-16 выглядит вот таким образом. Здесь мы видим все слои, что я и описывал раньше, только сама сеть определяет уже не 10 классов, как в нашем примере, а 1000. Слоёв свёртки здесь гораздо больше, и они могут идти друг за другом. Это нужно как раз для того, чтобы создать больше карт признаков и выделить больше деталей на каждой итерации.
Теперь, когда мы рассмотрели работу двух моделей на примере задачи классификации, мы можем двигаться дальше. Мы ведь хотим посмотреть, как нейросети увеличивают разрешение кадра в игре, а не просто угадывают цифры. Архитектуры сетей, к которым мы сейчас перейдём уже более сложные, но в их основе лежат те же принципы, которые мы только что рассмотрели. Поэтому, если вы сумели разобраться с функционированием этих двух моделей, вы сможете понять и происходящее далее.
Автоэнкодеры
Что ж, настало время поближе подобраться к архитектуре сети DLSS. Компания Nvidia не очень охотно делится подробностями работы своей модели, поэтому информации о ней в свободном доступе крайне мало. Нам доступна лишь общая концепция, тип архитектуры и краткое описание данных, которые подаются на вход сети. Однако, команда Facebook* Reality Labs разработала свою модель, которая решает ту же задачу, что и сеть Nvidia. Кроме того, они сделали полное описание своего подхода и выложили его в общий доступ. Их документация вкупе с тем, что мы уже знаем о нейронных сетях, поможет нам понять, как работает сеть DLSS. Начать предлагаю с того, что нам даёт сама Nvidia. На официальном сайте компании есть страничка, кратко объясняющая что такое DLSS и для чего применяется эта технология. Здесь мы можем видеть название архитектуры, которая лежит в основе модели — это Convolutional Autoencoder, ну или же «свёрточный автоэнкодер». Про свёрточные сети мы уже знаем, а что за автоэнкодер такой? А это довольно интересная сеть, на самом деле. В ранее рассмотренных нами моделях количество нейронов на выходном слое отличалось от входного в меньшую сторону из-за особенности задачи, которую мы ставили перед сетью. В автоэнкодере же количество нейронов на выходном слое может быть равно количеству нейронов на входном, и даже превышать его.
Автоэнкодер состоит из двух частей: кодера и декодера. Они соединяются между собой в месте под названием «bottleneck» — «бутылочное горлышко», которое является главной особенностью такого типа сетей. Первая часть сети — кодер, принимает на вход какой-то набор данных и сжимает его размер. Этот процесс так и называется — кодирование. В результате мы получаем наши данные в виде небольшого вектора, который называется «вектор скрытого состояния». Вторая часть сети — декодер, выполняет обратное преобразование с целью получения нового набора данных, либо восстановлению данных к исходному виду. Давайте рассмотрим пример. У нас есть сеть автоэнкодер с 784 нейронами на входе, как и в примерах выше. Количество нейронов вектора скрытого состояния сделаем равным 50. Размер выходного слоя будет также 784, как и на входе. Если мы передадим на вход автоэнкодера изображение цифры с разрешением 28×28 пикселей, мы получим представление этого изображения в сжатом виде. После обратного преобразования декодером мы получим ровно ту же цифру, что и была на входе. Качество изображения на выходе немного ухудшилось по причине того, что вектор скрытого состояния способен хранить только значимую часть информации без сохранения мелких деталей
На этом моменте у вас наверняка возник логичный вопрос:
А зачем вообще сжимать данные, чтобы потом распаковывать их обратно?
Оказалось, что такой подход очень полезен в определённых задачах. Например, мы можем обучить автоэнкодер убирать шум и артефакты на изображении. Для этого при обучении нужно сравнивать полученный результат с таким же изображением цифры без шума. В дальнейшем при передаче на вход автоэнкодеру изображение цифры с каким-то шумом или артефактами, на выходе мы получим чистое изображение без искажений. Качество и чёткость получаемых изображений, к слову, можно улучшить, если заменить текущую архитектуру сети на свёрточную модель автоэнкодера, а также увеличить размер вектора скрытого состояния. В качестве примера также можно привести и RTX Voice от Nvidia.
Если записанный звук представить в виде спектра на изображении, его можно обработать свёрточным автоэнкодером как обычную картинку. Когда пользователь передаёт на вход обученной модели свой голос с нежелательным шумом на фоне, она убирает из звука всё лишнее и на выходе получается очищенная запись голоса.
Это всё, конечно, здорово, но теперь вопросов стало ещё больше. Как автоэнкодер позволяет декодировать настолько сжатые данные до прежнего состояния? Как он хранит закодированные данные? И что ещё интереснее — как он позволяет увеличить разрешение изображения? Ведь мало того, что нужно увеличить количество пикселей, так ещё и сделать это из закодированного — сжатого состояния. Давайте сначала разберёмся с первыми двумя вопросами, а к последнему вернёмся чуть позже.
Успешное декодирование данных из вектора скрытого состояния — это во многом результат правильного подхода к обучению автоэнкодера, который отличается от того, что мы рассматривали ранее. По сути, основная задача заключается в том, чтобы уловить определённые закономерности сигнала на входе и как можно точнее восстановить его. Достигается это правильной корректировкой весов обеих частей сети. Обучение автоэнкодера можно осуществлять несколькими способами. Например, мы можем в качестве правильного ответа использовать то же изображение, что мы передали на вход. Затем с помощью функции нахождения минимума среднего квадрата ошибки попиксельно сравнить полученный результат с исходным, чтобы скорректировать веса каждого нейрона. Однако, такой подход далеко не всегда эффективен, поэтому специалисты по машинному обучению придумали другой способ. Для сравнения исходного изображения с результатом автоэнкодера стали использовать другую нейронную сеть, которую обучают попиксельному сравнению изображений. По сути, получается как бы две независимых сети в одной, которую называют «генеративно-состязательной сетью» или же Generative Adversarial Network. Такая сеть состоит из двух частей: генератора и дискриминатора. Генератор создаёт какой-то сигнал, например, изображение, а дискриминатор сравнивает его с эталоном и выдаёт ответ, на основе которого сеть-генератор обучается. Дискриминатор представляет собой обычную сеть с классификатором и имеет на выходе два нейрона, которые имеют значения «Real» или «Fake». Особенность генеративно-состязательных сетей состоит в том, что генератор и дискриминатор должны обучаться совместно. Если дискриминатор умеет хорошо верифицировать данные, а генератор только учится создавать их, то последний будет постоянно получать сообщение о плохом результате и не сможет обучиться корректировать ошибку. И наоборот, необученный дискриминатор будет вести генератор по неправильному пути. Работу таких сетей обычно описывают довольно понятным примером с фальшивомонетчиком и полицейским. Первый учится печатать поддельные купюры, а полицейский — отличать подделку от оригинала. Чем более успешен фальшивомонетчик в своём ремесле, тем сложнее полицейскому делать свою работу, поэтому и он должен совершенствовать свои навыки. DLSS на этапе обучения также представляет собой генеративно-состязательную сеть, но гораздо более сложную. Генератор в виде автоэнкодера получает на вход изображение низкого разрешения и некоторые другие данные, на основе которых обучается создавать картинку более высокого разрешения. Дискриминатор выполняет оценку результата и сообщает генератору какие изменения нужно сделать, чтобы более эффективно выполнять работу. Обученная модель уже не требует оценки работы дискриминатором, поэтому пользователь получает с драйвером только сам генератор.
Что касается хранения данных в векторе скрытого состояния, то это довольно сложный для понимания вопрос. Рассмотренный ранее автоэнкодер, который восстанавливает изображение цифры до исходного, имеет на входе 784 нейрона, каждый из которых содержит значение яркости отдельного пикселя на изображении. Кодер сжимает эти данные, получая новое представление, которое находится в пятидесяти нейронах вектора скрытого состояния. Если попытаться визуализировать то, с чем работает автоэнкодер, то каждая картинка с его точки зрения представляет собой некоторую область в 784-мерном пространстве. Большая часть этого пространства не будет содержать никакой полезной информации, то есть, это просто шум. Когда кодер выполняет преобразование данных изображения в компактное представление вектора скрытого состояния, он пытается найти последовательность точек в сформированном пространстве, которое позволит воссоздать это изображение в будущем. После преобразования получается вектор из 50 элементов, который описывает некоторую 50-мерную поверхность в этом пространстве. Эта поверхность как раз и является представлением нашей цифры в скрытом пространстве, которое можно развернуть обратно в исходное изображение с помощью декодера. Чтобы лучше понять происходящее, давайте уменьшим размерность вектора скрытого состояния до двух нейронов, а затем пропустим через кодер набор данных MNIST из множества рукописных цифр, который мы рассматривали ранее. Кодер выполнит преобразование каждого изображения цифры в собственное представление скрытого пространства, что на выходе даст множество точек, описывающих эти цифры. Пространство этих точек мы можем отобразить на плоскости и получим примерно такую картину. Что из этого вообще можно понять? Если мы вернёмся к примеру распознавания цифр, то вспомним, что каждая цифра имеет конкретный уникальный набор активаций нейронов сети. Цифра 5, например, может быть написана множеством способов, но сеть всё равно понимает, что на вход мы даём именно пятёрку. В случае с автоэнкодером точки вектора скрытого состояния, описывающего пятёрку, попадут в какую-то конкретную область в этом пространстве. А поскольку цифру пять описывает конкретный набор активаций в сети, данные о других пятёрках окажутся в этой же области на относительно небольшом расстоянии друг от друга. Получается, что данное пространство представляет области точек всех цифр, которые мы передавали для обучения этой модели. В случае с задачей классификации сеть выполняет деление этого пространства на множество точек для каждого класса и ответом, по сути, является то, в какую область попадает та или иная цифра. Если мы выберем какую-то произвольную точку в пространстве, указав нужные значения в векторе скрытого состояния, мы сможем пропустить этот вектор через декодер. В результате мы получим декодированное изображение цифры, если мы попали в область точек, которые её описывают. При попадании в точку за пределами этой области, мы получим полную ерунду на выходе. Этот пример может натолкнуть нас на некоторые интересные мысли. Цифра представляет собой осмысленное сочетание пикселей, которое провоцирует конкретный шаблон активаций нейронов. А вот шум, напротив, будет отличаться на каждом изображении, а значит, его явные признаки выделить не удастся. Получается, что шум на изображении не попадает ни в одну из групп точек, описывающих цифры в этом пространстве, а значит, не будет сохранён в векторе скрытого состояния. Вот почему развернув обратно такой вектор сеть выдаст чистое изображение без шума. Разумеется, для этого нужно обучить сеть выполнять такую операцию.
Представить себе способ хранения информации автоэнкодером довольно сложно, но так ли это важно, если сеть выполняет поставленную задачу? Можно называть это «магией» нейронных сетей, если хотите, которая просто работает. Теперь остаётся понять главное — как эта «магия» позволяет получать изображения высокого качества. Именно этому вопросу и посвящена последняя часть этого материала.
Сети повышения размерности
Начать стоит с того, что глобально задача повышения разрешения используется в двух случаях: улучшение изображения на базе одного исходного, либо на базе последовательности исходных изображений.
Первый используется в тех случаях, когда у нас есть какой-то рисунок или фото, а второй — для видеофайлов или набора кадров в игре. В каждом из вариантов используется уникальный подход, потому как количество доступных входных данных различно. Если у нас имеется одно изображение, то нейросеть может использовать только те данные, что представлены на нём. Для улучшения видео требуются уже более сложные алгоритмы, поскольку для обработки доступна последовательность нескольких кадров, однако и результат на выходе можно получить лучше. В случае с играми имеется самое большое количество данных для обработки, плюс, само изображение формируется в реальном времени, а значит, на его качество можно повлиять в процессе создания. Рассматривать работу с видео мы не будем, но затронем работу с одним изображением, поскольку это нам потребуется для понимания далее.
Для задач повышения размерности изображений также используются свёрточные нейронные сети, только их архитектура заметно усложняется. Если ранее мы рассматривали случаи с последовательной свёрткой и последующим представлением карт признаков в одномерный вектор, то для увеличения разрешения сеть по сути выполняет обратное преобразование всех этих карт в финальное изображение. Для этого также используются слои свёртки, только работают они в данном случае немного иначе.
Процесс повышения размерности называется транспонированной свёрткой — Transposed Convolution. Как и в случае с обычной свёрткой, карты признаков обрабатываются фильтрами — небольшими матрицами, которые проходят по всему изображению. Эти матрицы — ядра свёртки, попадают на небольшую область и перемножают значения пикселей изображения на значения матрицы. Ключевую роль в понимании процесса свёртки играют понятия stride и padding, которые ранее мы не рассматривали. Их использование может варьироваться от задачи к задаче, поскольку специалисты используют разные подходы к созданию карт признаков. Свёртка может осуществляться несколькими способами, которые вы сейчас можете наблюдать, и каждый из них хорош в отдельных ситуациях.
К примеру, если входное изображение имеет равное количество пикселей с выходным на конкретном слое или требуется более тонкая обработка краёв изображения, ядро смещают так, чтобы оно выходило за пределы входного изображения. При этом требуется создать «контур» с «фальшивыми» пиксели с нулевыми значениями, чтобы ядро могло их обработать. Количество таких «контуров» и определяет параметр padding.
Если же исходное изображение имеет больше пикселей, чем финальное на слое, требуется определённым образом перемещать ядро свёртки в зависимости от того, насколько требуется уменьшить карту на конкретном слое. К примеру, в такой ситуации выполняется свёртка для области 5×5 пикселей, а на выходе получаем область 2×2. В таком случае нужно скорректировать шаг свёртки путём пропуска отдельных пикселей при движении. Здесь вы можете видеть, как ядро свёртки перемещается на не 1 пиксель, а сразу на два, это и определяет параметр stride. Далее вы ещё увидите, как это работает.
Для повышения размерности т. е. создания карт большего разрешения из карт с меньшим, требуется немного иначе использовать операцию свёртки. Для простоты понимания давайте выделим два основных случая: когда пиксели карты меньшего разрешения сгруппированы в центре, и когда её пиксели равномерно распределяют по области с добавлением нулевых пикселей между ними
В первом случае возможностей для создания новых пикселей не так уж и много, особенно в центре, поэтому давайте посмотрим, что можно сделать, используя второй вариант. Имея набор пустых пикселей вокруг заданного, мы можем назначить им какие-то значения, но откуда эти значения взять? Способов сделать это довольно много, но давайте сначала рассмотрим базовые.
Простейший из них подразумевает простое копирование цвета соседних пикселей. Как вы понимаете, качество при таком методе интерполяции будет отвратительное и, по сути, мы получим то же изображение низкого разрешения, но с большим количеством пикселей
Ещё один способ — это рассчитать средневзвешенное значение цвета на основе окружающих пикселей. Если у нас имеется, скажем, 10 пикселей, а цвет известен только для первого и последнего, то значения остальных можно вычислить на основе общего количества пикселей. Именно это и происходит, когда вы делаете градиентную заливку в том же Photoshop’е, например. Этот метод называется линейной интерполяцией. В случае с изображением, вычисления нужно производить как по оси X, так и по оси Y, поэтому интерполяция в этом случае будет являться билинейной.
Значение цвета пикселя определяется на основе средневзвешенного цвета окружающих пикселей в квадрате 2×2, поэтому результат получается лучше. Если значение цвета конечного пикселя определять на основе среднего в квадрате 4×4 пикселя, то интерполяция будет называется бикубической.
Это, кстати, наиболее популярный способ, ввиду оптимального соотношения производительности и качества. Его использует видеокарта для масштабирования изображения, когда пользователь выставляет внутреннее разрешение в игре меньше рекомендуемого для его монитора. Несмотря на то, что бикубическая интерполяция справляется с задачей увеличения разрешения очень неплохо, она не решает проблему низкого его качества и замыливания, в чем несложно убедиться самостоятельно. Кроме того, в случае нейронных сетей при использовании транспонированной свёртки проявляется ещё один неприятный эффект — артефакт шахматной доски. На этом изображении его довольно неплохо видно.
Он возникает из-за особенностей работы самого свёрточного слоя, в котором для получения цвета рядом стоящих конечных пикселей измерение производится на основе некоторого количества общих исходных пикселей, из-за чего происходит как бы наслоение одних данных на другие. Естественно, это негативно сказывается на итоговом изображении. Решение для этой проблемы предложили специалисты по машинному обучению из компании Twitter. Они разработали свой метод, который называется sub-pixel convolution, или сабпиксельная свёртка. Этот метод добавляется в сеть и работает как обычный слой свёртки. Как мы помним, в процессе работы с изображениями слои свёртки генерируют множество карт признаков, из которых затем в обратном порядке выполняется реконструкция изображения. На каждом слое происходит выборка пикселей из карт их значений и умножение на подобранные в процессе обучения коэффициенты матрицы свёртки. Сабпиксельная свёртка подразумевает несколько иную работу с картами признаков для повышения разрешения. На первом этапе, как я и показывал выше, пиксели карты меньшего разрешения размещаются на карте большего размера с промежутками. Здесь белый цвет обозначает значимые пиксели, а серый — пиксели с нулевыми значениями. Далее значение конкретного пикселя собирается с нескольких других карт — каналов, после чего они отображаются на определённые позиции вокруг искомого пикселя на конечной карте специальным алгоритмом.
Полученный результат можно использовать как одну из карт признаков следующего подобного слоя и так далее. В качестве примера можно привести сеть SRResNet, где как раз используется подобный подход.
Если вы всё ещё удивлены как банальным копированием пикселей получается повысить качество картинки, то есть ещё две вещи которые стоит знать о таких сетях. При внимательном осмотре схемы этой сети в глаза бросаются вот эти соединения. Это особенность сетей типа residual — так называемых «остаточных» сетей. Логика в том, что результаты, полученные на каждом слое свёртки при понижении размерности можно передать на вход последующим слоям напрямую, что помогает дополнительно улучшить результат работы сети. Кроме всего прочего, очень важную роль играет процесс обучения сети. В нём для оценки выходного изображения применяется попиксельный анализ изображения и сравнение с эталоном несколькими способами. К примеру, первым может быть определение минимума среднего квадрата ошибки между результатом и эталоном по каждому пикселю, вторым — оценка изображения сетью-дискриминатором ну или вычисление суммы всех квадратов ошибки между пикселями и нахождение среднего значения. Ну и не стоит забывать о метриках типа PSNR — соотношение полезного сигнала к шуму.
В работе с изображениями, к слову, важно не только хорошее значение PSNR, поскольку оно не отображает целостность восприятия информации на изображении. Для этого была изобретена специальная метрика SSIM, обозначающая структурное сходство изображений. Именно этот параметр играет ключевую роль в восприятии изображения человеком: чем он выше, тем больше изображение соответствует правильному. В процессе обучения на множестве изображений высокого разрешения, сеть постепенно подбирает правильные значения весов, и с каждой итерацией её результат становится лучше.
Пространственно-временнóе масштабирование кадра
С подходом повышения разрешения на базе одной картинки мы разобрались, осталось понять, что происходит с изображениями, которые создаются игровым движком. Тут ситуация гораздо интереснее. Если в первом случае мы могли работать только с готовым изображением, пытаясь увеличить исходное количество информации, то при интеграции нейронной сети с игровым движком у нас есть доступ к данным, использующихся в создании этого изображения. Для улучшения игрового кадра используются несколько источников информации: сам игровой кадр с низким разрешением, буфер глубины, буфер с векторами движения и буфер истории кадров.
Значения цвета в буфере глубины показывают, насколько каждый пиксель удалён от игровой камеры в 3D-сцене. Буфер с векторами движения содержит информацию о смещении каждого пикселя текущего кадра относительно предыдущего. Буфер истории содержит один или несколько предыдущих кадров, данные из которых помогут выполнить реконструкцию текущего кадра.
Чтобы разобраться как это всё работает, рассмотрим сеть команды Facebook Reality Labs, о которой я говорил выше. Её архитектура включает в себя три независимые подсети, каждая из которых выполняет определённый набор действий, и несколько других этапов обработки. Рассмотрим пример, в котором мы хотим получить кадр с разрешением 4К, выставив в настройках DLSS режим «производительность». В таком случае на вход сети отправится изображение с разрешением 1920×1080, содержащее 2 073 600 пикселей. Нейросеть в итоге должна увеличить количество пикселей кадра до 8 с лишним миллионов, что в 4 раза превышает исходное. Кроме того, нужно учитывать особенности работы со сгенерированными в процессе рендера изображениями. На готовом изображении информация о геометрии объекта по большей части присутствует и вопрос только в качестве и чёткости самого изображения. В случае с рендером 3D-сцены, который является проекцией её на двухмерное изображение, нужно ещё и восстановить недостающие данные о геометрии сцены. Тот пример, о котором я говорил в начале, хорошо показывает, что сеть должна определить значения недостающих пикселей для построения изображения высокого качества. Происходит это вот как.
Процесс начинается с подачи на вход сети игрового кадра пониженного разрешения, в нашем случае 1920×1080. Полученное изображение обрабатывается двумя способами, каждый из которых преследует определённую цель. Сначала изображение переводится из цветовой схемы RGB в LAB.
LAB — это аббревиатура названия двух похожих цветовых схем, где «L» означает Lightness — яркостную составляющую, а «a» и «b» — хроматические составляющие, которые отвечают за цвет.
В одной из схем это красный и синий цвета, в другой — жёлтый и зелёный. Делается это обычно для лучшего сжатия изображения и большей скорости обработки. Человеческий глаз более чувствителен к изменению яркости, чем к изменению цвета, поэтому цветовые каналы можно обрабатывать грубее. Такой же принцип используется для сжатия изображения в формате JPEG.
После этого следует этап Feature Extraction — выделение признаков. На вход первой из трёх подсетей передаётся 4 изображения: карта из буфера глубины и три канала игрового кадра в цветовой схеме LAB.
Эта небольшая свёрточная сеть создаёт 12 карт признаков — каналов, которые получаются объединением 8 карт, полученных непосредственно в процессе свёртки, с 4 каналами входных данных. Следом идёт процесс, названный разработчиками Zero Upsampling. Это, по сути, тот же процесс, что уже описывал выше, когда пиксели меньшего изображения размещают на большем с промежутками из нулевых пикселей. Отличие только в том, что для нулевых пикселей никакие значения не определяются, поэтому изображение после этого процесса выглядит вот так.
Насколько я понял, эта операция выполняется для всех 12 каналов, полученных на выходе первой подсети, после чего они отправляются на вход сети реконструктора, о которой чуть позже. Также Zero Upsampling применяется и к самому исходному кадру низкого разрешения, а результат отправляется на вход второй подсети, отвечающей за пересчёт весов. Об этой сети мы сейчас поговорим подробно, но перед этим посмотрим какие ещё данные передаются ей на обработку. На вход этой сети подаются обработанные данные предыдущих кадров, которые предварительно проходят 3 этапа. Первые два мы уже рассматривали — это выделение признаков и Zero Upsampling, а вот третий довольно любопытный. Backward Warping переводится на русский примерно как обратная деформация или искривление. Суть этого этапа в определении смещения пикселя одного кадра относительно его предшественника, для чего используют карту из буфера векторов движения. Этот процесс называется «временной репроекцией». Он имеет довольно много нюансов и сложностей из-за ситуаций, когда рассматриваемый пиксель текущего кадра отсутствует в предыдущем.
Например, когда при повороте камеры мы видим объект, которого не было в предыдущем кадре, либо часть одного объекта стала перекрываться другим при смене кадра. Временная репроекция выполняется для пикселей каждого из нескольких кадров истории с накоплением данных. Накопление позволяет просуммировать общее смещение одного пикселя между несколькими кадрами и получить на выходе искажённое изображение, которое понадобится далее. Результат этой операции выглядит вот та
Далее следует блок Feature Reweighting — этап повторного взвешивания карт признаков, который выполняется второй подсетью. Она берёт обработанные данные из нескольких прошлых кадров и объединяет их особым образом. Тут логично задаться вопросом: «А как вообще прошлые кадры помогают выполнять реконструкцию изображения и сглаживание? Что такого особенного там содержится?». Подобный способ улучшения изображения называется Spatial-Temporal Super-Sampling — пространственно-временной супер-сэмплинг. Называется он так потому, что в отличии от методов для одиночных изображений или видео мы работаем не просто с набором пикселей. В случае с игровым рендером мы работаем с ракурсами камеры, которая перемещается в пространстве, а информация в буферах глубины или векторов движения — это лишь способ удобного хранения этих данных. Ключевыми элементами этого метода является репроекция пикселей и накопление данных из прошлых кадров, которые позволяют увеличивать количество сэмплов. Только делают это не грубой силой, как в случае с MSAA, например, а иным путём. При использовании MSAA цвет пикселя по краям объектов определяется не одной выборкой, а двумя или более, в зависимости от выбранного пользователем коэффициента. Это заметно увеличивает нагрузку на видеокарту в каждом кадре. Методы пространственно-временной реконструкции также используют несколько выборок, только берут их из прошлых кадров, что существенно экономит производительность. Тут появляется ещё два интересных вопроса: «Откуда берутся дополнительные выборки, если положение выборки одного пикселя в двух кадрах будет одинаковым? И если этот метод полагается на постоянное перемещение камеры, откуда брать данные, если пользователь не перемещает камеру либо она и вовсе статична?». Генерация выборок достигается методом так называемого «дрожания» камеры — jitter. При рендере каждого кадра используется одна выборка на пиксель, но её положение сменяется между кадрами за счёт незаметного для пользователя небольшого смещения камеры. Выборка, находящаяся в центре пикселя, совпадает с его центром, поэтому её часто называют «центроидом» пикселя
Методы DLSS и TAA используют числовую последовательность Холтона для изменения положения центроида между кадрами. Анимация, которую вы сейчас можете наблюдать, показывает смену положения центроидом в разных кадрах.
Это смещение как раз достигается дрожанием камеры, которая двигается согласно этой последовательности. Это позволяет получить разный набор данных в одном пикселе в нескольких кадрах, как вот здесь, например:
После накопления достаточного количества таких сэмплов из предыдущих кадров появляется возможность выбирать наилучшее значение для пикселя текущего кадра. Также необходимо проанализировать смещение пикселя и сделать репроекцию, чтобы избавиться от так называемого ghosting-эффекта, из-за которого мы можем наблюдать шлейфы в играх. Для этого используют отбраковку плохих значений пикселя в буфере истории — history rectification. Чтобы это сделать, нужно выполнить взвешивание значений этих пикселей, переместить пиксель прошлого кадра на необходимую позицию и выбрать наиболее подходящую в конкретном случае выборку. В сглаживании TAA такой анализ выполняется по определённому алгоритму, который примерно одинаков для всех пикселей. Нейронная сеть же позволяет более гибко работать с изображением, подбирая наиболее эффективный вариант в каждом конкретном случае. Именно этот набор операций и проделывает сеть повторного взвешивания, генерируя на выходе 4 карты весов для каждого пикселя, которые используется на финальном этапе обработки.
Для реконструкции и повышения разрешения специалисты Facebook Reality Labs использовали сеть U-Net, разработанную отделением Computer Science Фрайбурского университета.
U-Net — это свёрточная сеть, использующая концепцию остаточных сетей. Часто она применяется для выделения объектов на изображении, так называемой семантической сегментации, останавливаться на которой мы сейчас не будем. Эта сеть принимает на вход данные, полученные на предыдущих этапах, и создаёт на выходе три изображения, которые являются цветовыми каналами RGB. По сути, сеть выполняет те же действия, что мы рассматривали ранее в алгоритме сабпиксельной свёртки. Отличия лишь в том, что значения нулевых пикселей определяются не из имеющихся данных исходного кадра в низком разрешении, а на основе карт весов пикселей из предыдущих кадров. Именно это и позволяет получать очень качественный результат на выходе. Пока вы смотрите на результаты работы сети команды Facebook, я дам некоторые пояснения по сети DLSS от Nvidia. Как я и говорил, подробной информации о её работе в свободном доступе нет, однако, на основе полученной информации мы можем спроецировать этапы работы с изображением и на сеть DLSS. Nvidia указывает свёрточный автоэнкодер в качестве модели своей сети, и я полагаю, что они используют его вместо U-Net для реконструкции кадра. На основании недавно выпущенной статьи про DLSS самой Nvidia можно сделать вывод, что этап повторного взвешивания также реализован похожим образом, и реконструкция кадра осуществляется на основе карты весов для пикселей. В остальном отдельные этапы также вполне могут быть разбиты несколько отдельных алгоритмов или небольших сетей, но вряд ли общая концепция заметно отличается.
Разница между версиями DLSS
Перед тем, как мы перейдём к заключению, расскажу о некоторых отличиях DLSS первой версии от второй, о которой и шла речь в этом ролике. Редакция ресурса DTF проводила интервью с техническим менеджером Nvidia Олегом Шкодой. В нём он рассказал о тернистом пути, который прошла технология DLSS в процессе разработки. Как оказалось, первая версия сети обучалась индивидуально для каждой игры, а в случае с игрой Control и вовсе использовался иной алгоритм. Первая версия DLSS показала себя не очень эффективно во многом по причине индивидуального обучения под каждую игру, потому как результат обучения нужно сохранять и отправлять пользователям вместе с драйвером. Размер файлов обученной модели и её сложность в таком случае увеличивались бы с каждой игрой, а скорость её работы снижалась. По этой причине было принято решение переработать архитектуру сети. Можно, конечно, сказать, что Nvidia поторопилась и выкатила сырую технологию, но дело в том, что такие комплексные вещи часто получаются не с первой итерации. Учитывая, что Nvidia была одной из первых компаний, предложившей готовое программно-аппаратное решение, даже такой результат был далеко не лишним. Кроме того, переход на версию 2.0 был программным и не требовал от пользователей покупки новых видеокарт.
В DLSS 2.0 используется совершенно иная архитектура, и модель обучается уже не только на игровых данных, но и на реальных изображениях. По крайней мере, на сайте Nvidia заявлено именно это. Пользователям стоит помнить, что, если бы первая версия DLSS не вышла в свет, не факт, что сейчас эта технология работала бы также эффективно. Нужно было выкатить какое-то решение, выявить его плюсы и минусы и подумать над улучшениями. Сейчас DLSS является очень удобным инструментом для разработчиков и добавить его в движок немногим сложнее, чем сглаживание TAA, потому как оба метода используют одни и те же данные для работы. Пользу для обычных игроков и вовсе трудно переоценить потому как DLSS позволяет не только играть в современные проекты с большей производительностью, но и продлить жизнь видеокартам среднего ценового сегмента. Начиная с осени 2020го года DLSS имеет версию 2.1 и позволяет масштабировать картинку до 9 раз, позволяя повысить разрешение, например, с 1280×720 аж до 4К.
Вот, пожалуй, и всё, что я хотел вам сегодня рассказать. Пишите, что думаете по поводу этого материала в комментариях и задавайте вопросы, если они остались.
Если вам понравился материал, обязательно ставьте поблагодарите автора в комментариях под его видео, ознакомьтесь с другими его не менее интересными работами. Также, в субботу, в 15:30 по МСК пройдёт прямая трансляция, где можно будет задать свой вопрос по этой теме и получить на него ответ.
https://www.youtube.com/watch?v=KULkSwLk62I
structural similarity
google super-res используется в камерах
SRResidualNetwork
https://neurohive.io/ru/vidy-nejrosetej/resnet-34-50-101/
image scaling
https://www.youtube.com/watch?v=fuTYqzWPHGg
U-Net и AutoEncoder
https://www.youtube.com/watch?v=d7VqnJWs0wk
https://towardsdatascience.com/understanding-latent-space-in-machine-learning-de5a7c687d8d
https://hackernoon.com/latent-space-visualization-deep-learning-bits-2-bd09a46920df
https://www.youtube.com/watch?v=iLoCVz3RJTc
https://www.youtube.com/watch?v=OSShk6jA_us
https://www.youtube.com/watch?v=pj9-rr1wDhM
https://arxiv.org/pdf/1603.07285v1.pdf
https://arxiv.org/pdf/1803.02735.pdf
https://arxiv.org/pdf/2102.06979.pdf
схемы свёртки
https://habr.com/ru/post/348000/
https://medium.com/@balovbohdan/%D1%81%D0%B2%D0%B5%D1%80%D1%82%D0%BE%D1%87%D0%BD%D1%8B%D0%B5-%D0%BD%D0%B5%D0%B9%D1%80%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5-%D1%81%D0%B5%D1%82%D0%B8-%D1%81-%D0%BD%D1%83%D0%BB%D1%8F-4d5a1f0f87ec
https://medium.com/@balovbohdan/%D0%B3%D0%BB%D1%83%D0%B1%D0%BE%D0%BA%D0%BE%D0%B5-%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5-%D1%80%D0%B0%D0%B7%D0%B1%D0%B8%D1%80%D0%B0%D0%B5%D0%BC%D1%81%D1%8F-%D1%81%D0%BE-%D1%81%D0%B2%D0%B5%D1%80%D1%82%D0%BA%D0%B0%D0%BC%D0%B8-6e47bfc27792
https://theaisummer.com/receptive-field/
https://distill.pub/2016/deconv-checkerboard/
https://github.com/vdumoulin/conv_arithmetic
про up-sampling
https://www.quora.com/How-do-fully-convolutional-networks-upsample-their-coarse-output
https://www.youtube.com/watch?v=ByjaPdWXKJ4&t=1020s
https://www.coursera.org/lecture/advanced-computer-vision-with-tensorflow/upsampling-methods-ku4yr
https://habr.com/ru/company/pixonic/blog/512770/
https://dspace.spbu.ru/bitstream/11701/12146/1/diplom.pdf
TENSOR RT
https://www.youtube.com/watch?v=6My-daDk4zE
https://www.youtube.com/watch?v=1bEqRvJrZgE
https://habr.com/ru/post/511340
CNN
https://www.youtube.com/watch?v=FmpDIaiMIeA
https://www.youtube.com/watch?v=ILsA4nyG7I0
https://www.youtube.com/watch?v=lthIsMLaq1Q
CNN visualization
https://www.cs.ryerson.ca/~aharley/vis/conv/
https://www.youtube.com/watch?v=f0t-OCG79-U
https://www.youtube.com/watch?v=AjtX1N_VT9E
NN visualization (upscale it)
https://www.youtube.com/watch?v=3JQ3hYko51Y
Self-driving car
https://www.youtube.com/watch?v=3GF0wUQMdXw
https://cgg.mff.cuni.cz/~jaroslav/papers/2018-mlrendering/slides/01-keller%20-%20from%20machine%20learning%20to%20graphics%20and%20back.pdf
Что такое машинное обучение и глубокое обучение
https://www.youtube.com/watch?v=OT1jslLoCyA&list=PLZbbT5o_s2xq7LwI2y8_QtvuXZedL6tQU&index=2
https://dtf.ru/hard/680207-bloomberg-uluchshennaya-model-switch-poluchit-podderzhku-dlss
OPENED TABS
The Neural Network, A Visual Introduction | Visualizing Deep Learning, Chapter 1
https://www.youtube.com/watch?v=UOvPeC8WOt8
Convolutional Neural Networks Explained (& Visualized)
https://www.youtube.com/watch?v=pj9-rr1wDhM
Types of convolution
https://www.youtube.com/watch?v=gmr18xg4wTg
Transposed Convolution
https://www.youtube.com/watch?v=96_oGE8WyPg
L16.3 Convolutional Autoencoders & Transposed Convolutions
https://www.youtube.com/watch?v=ilkSwsggSNM
Keras Lecture 4: upsampling and transpose convolution (deconvolution)
https://www.youtube.com/watch?v=QmCxqsbn5B0
Upsampling
https://www.youtube.com/watch?v=8jBySEOFjUw&t=527s
Vehicle Perception for my Self Driving Car
https://www.youtube.com/watch?v=3GF0wUQMdXw
Convolution 3D
https://www.cs.ryerson.ca/~aharley/vis/conv/
TAA article
https://community.arm.com/developer/tools-software/graphics/b/blog/posts/temporal-anti-aliasing
Temporal Anti Aliasing – Step by Step
https://ziyadbarakat.wordpress.com/2020/07/28/temporal-anti-aliasing-step-by-step/
* Деятельность родительской организации «Meta» признана экстремистской и запрещена на территории Российской Федерации

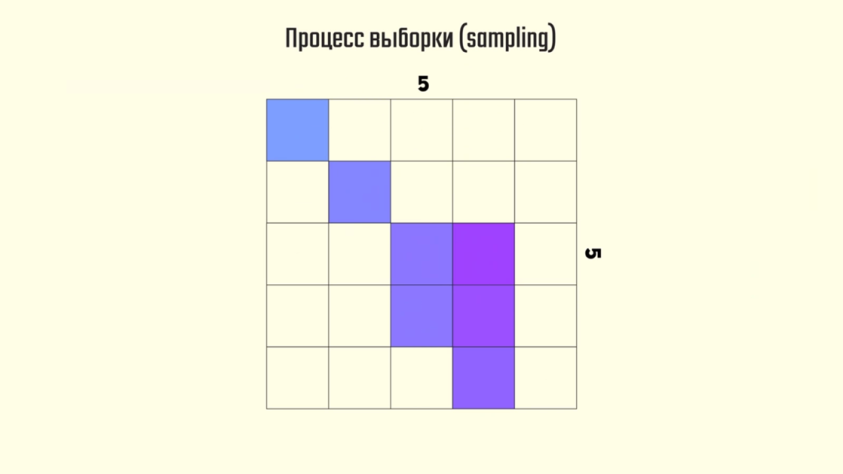


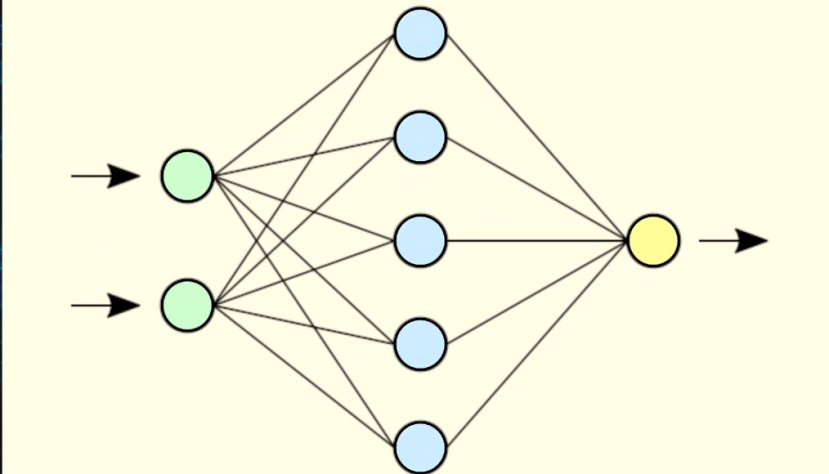
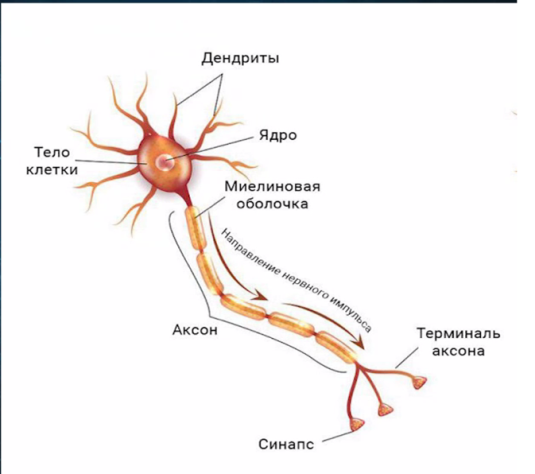
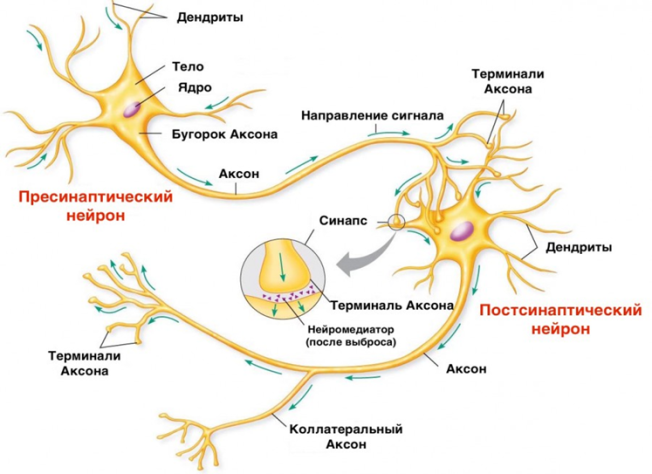


















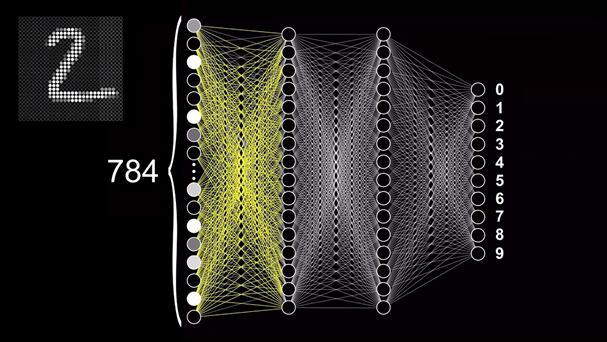
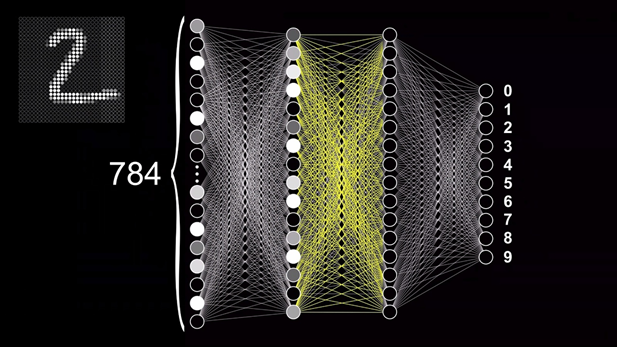
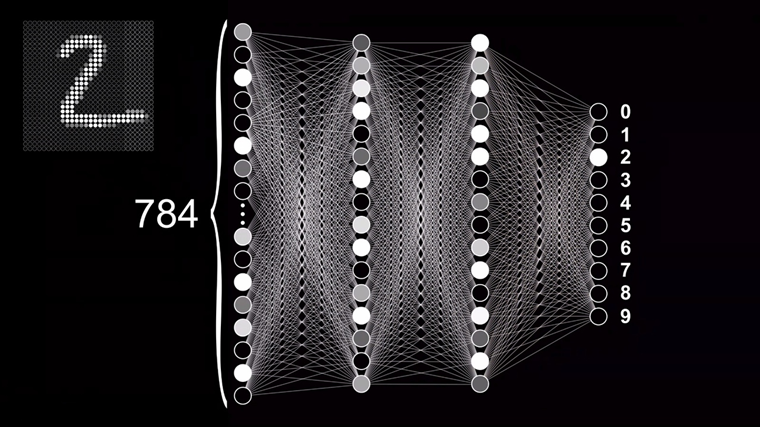


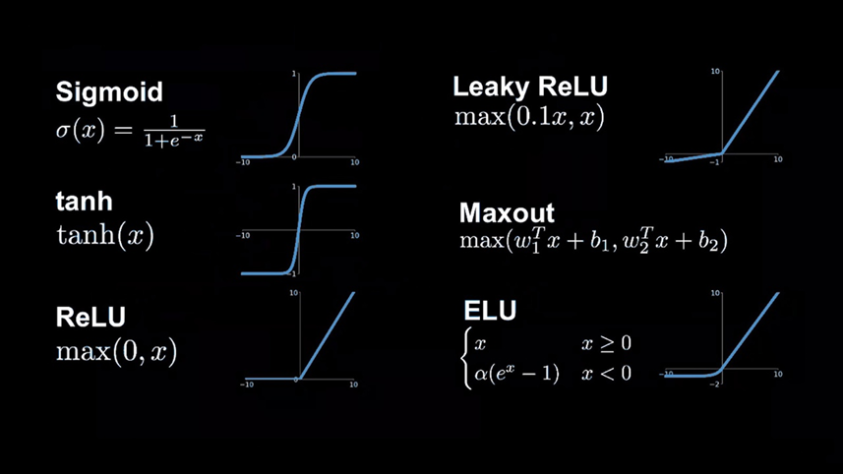
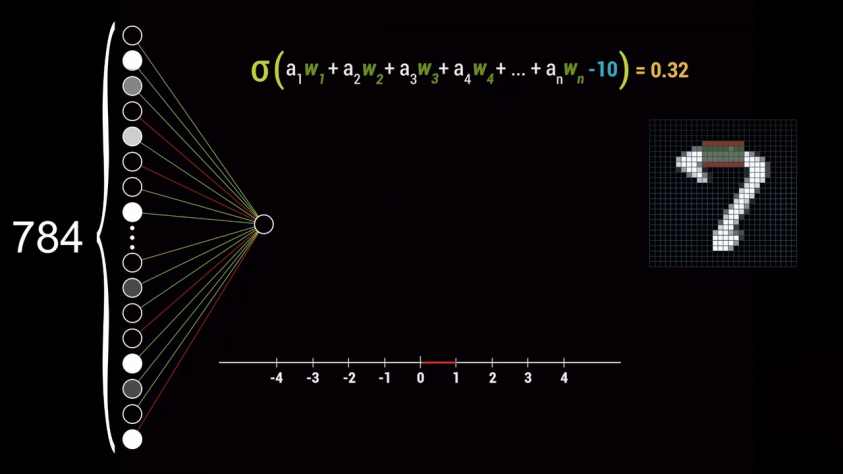
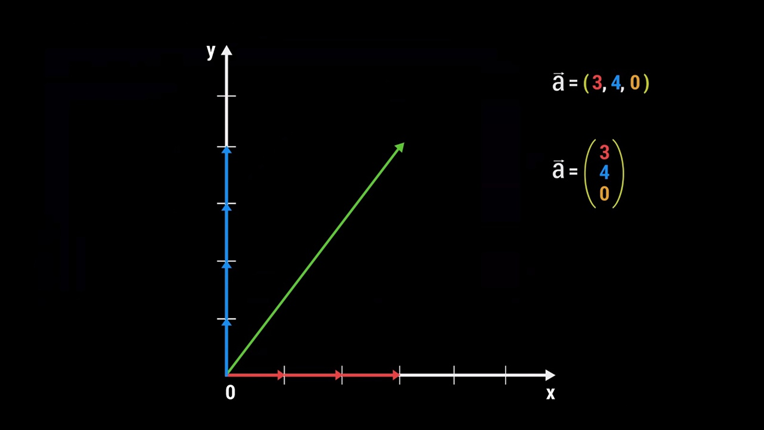
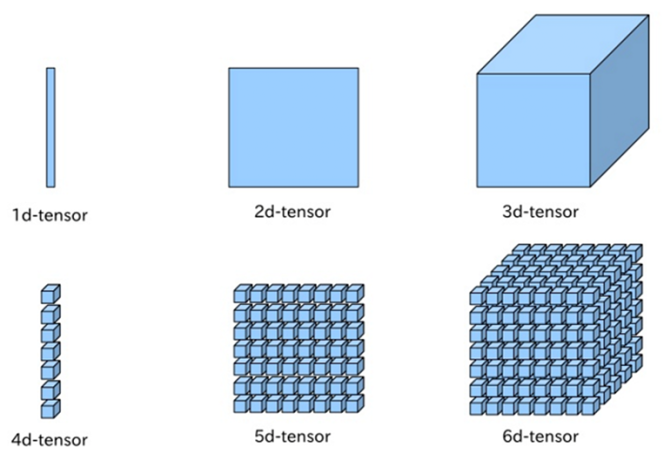
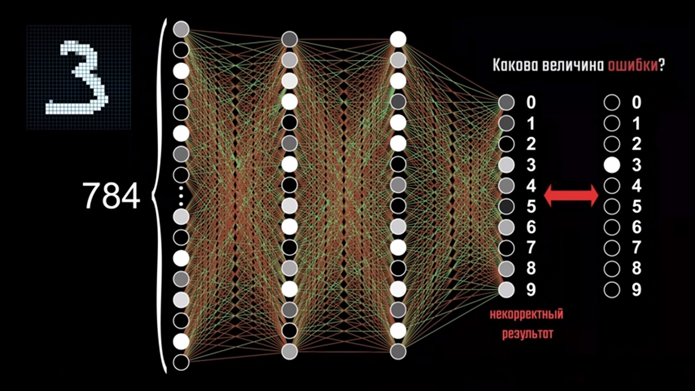
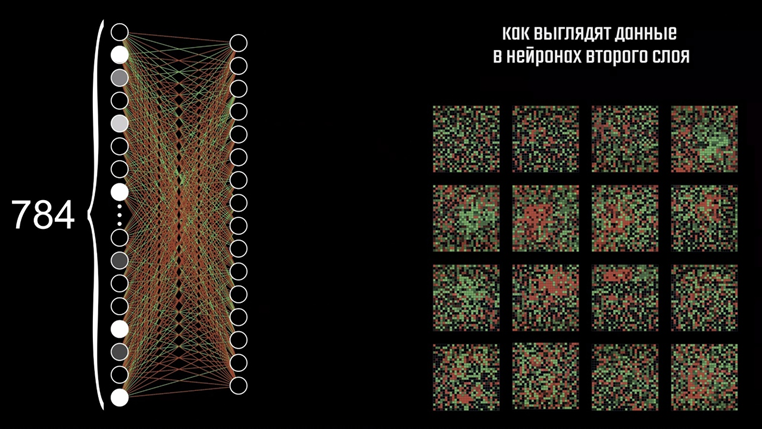



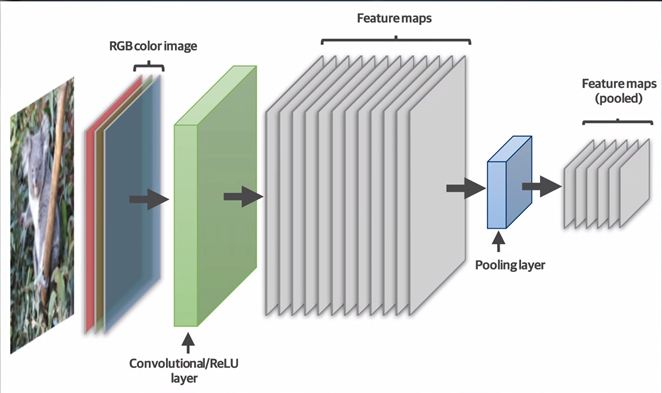
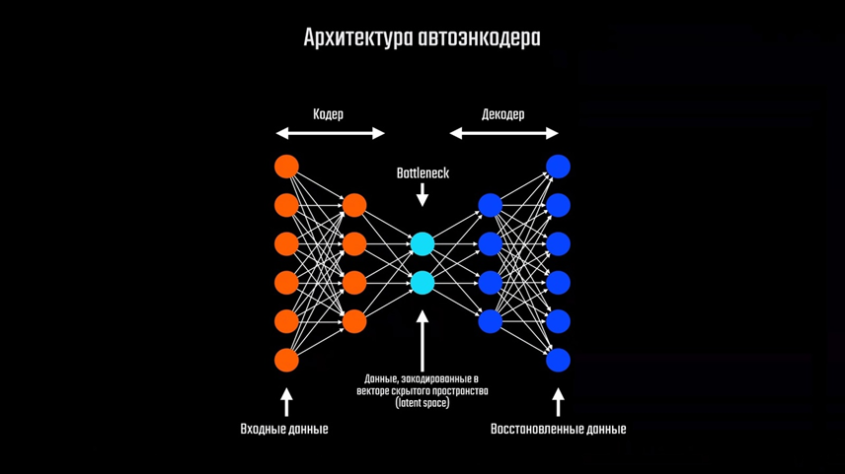
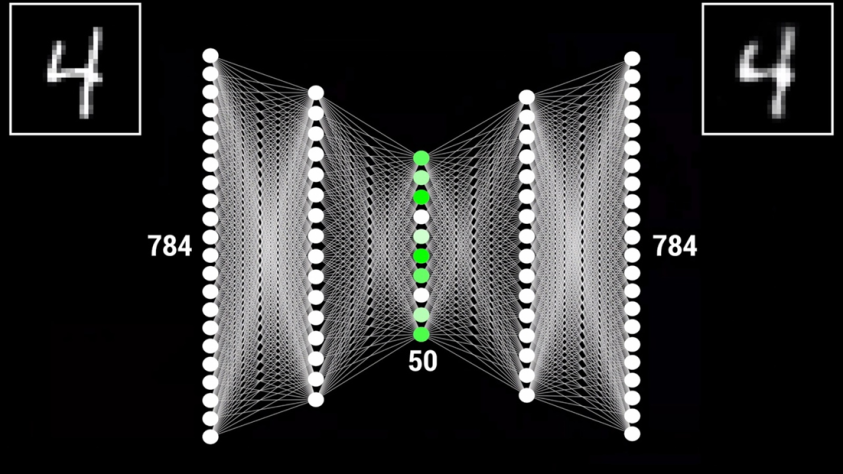
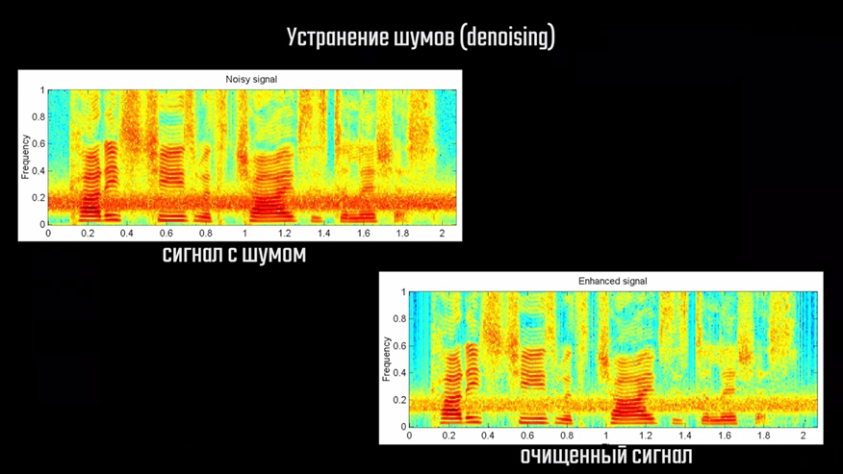
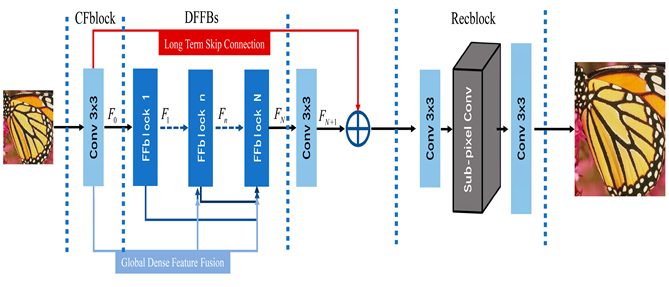
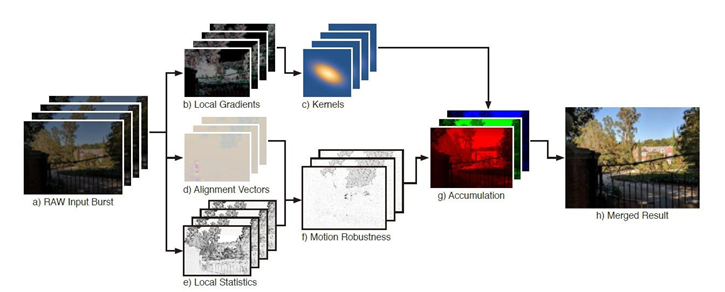
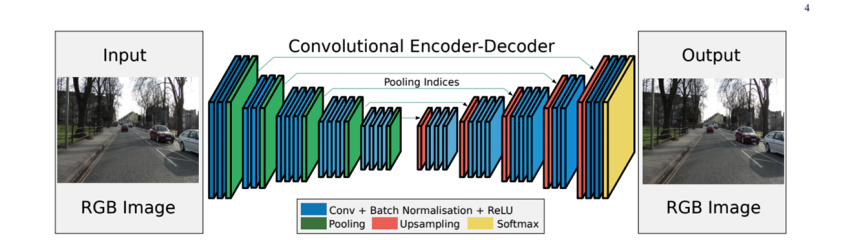
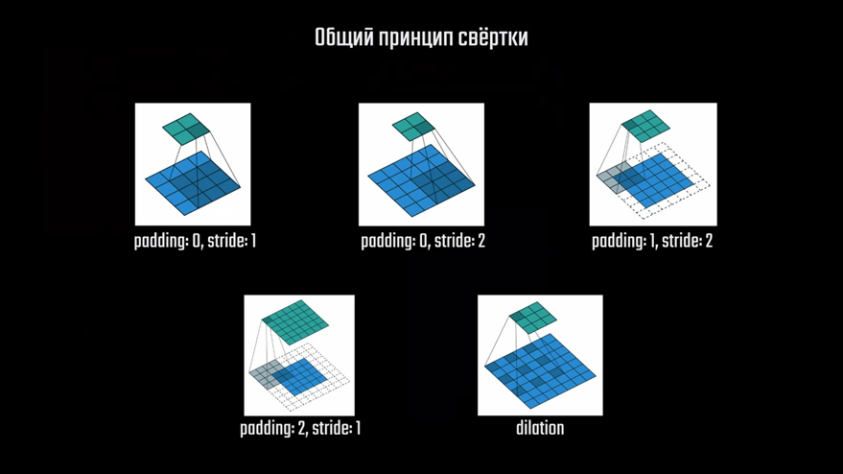




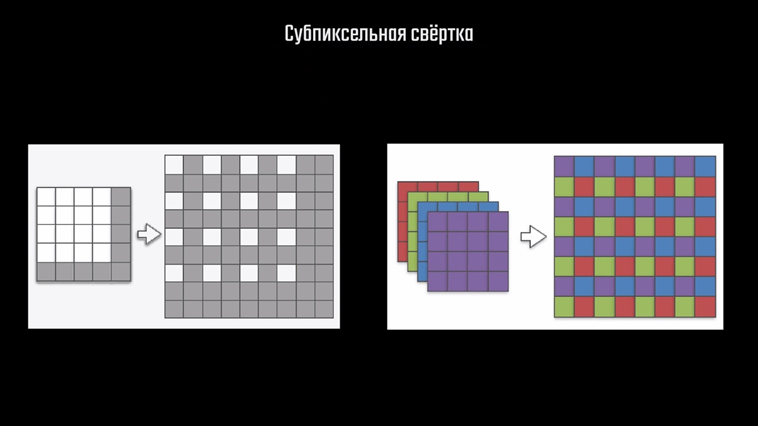
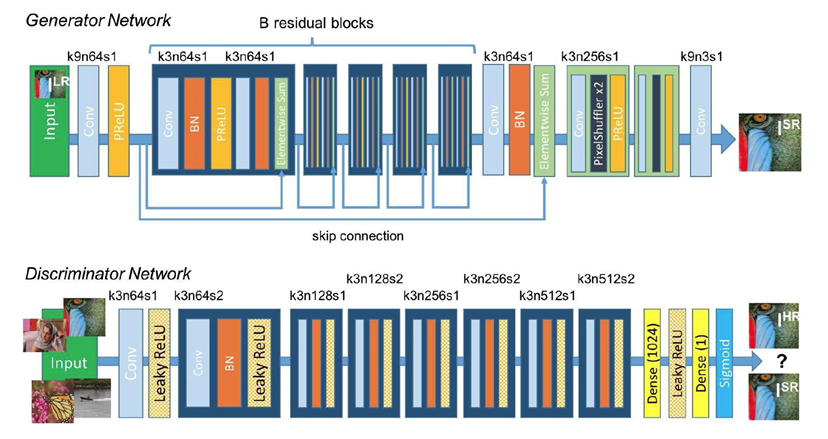


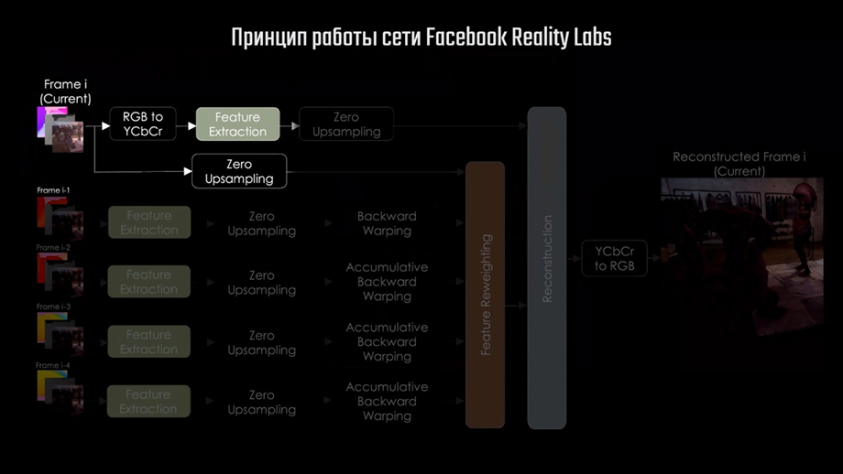
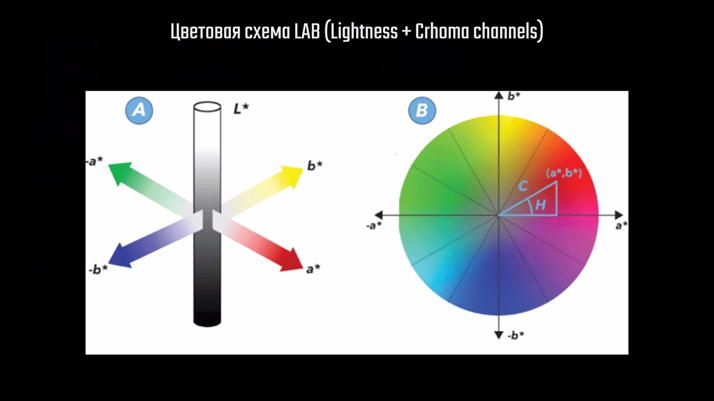
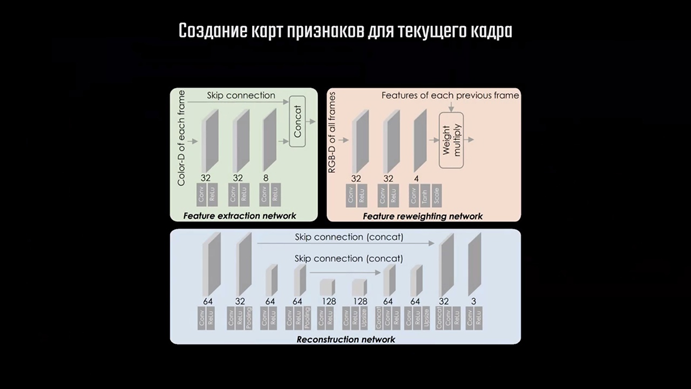
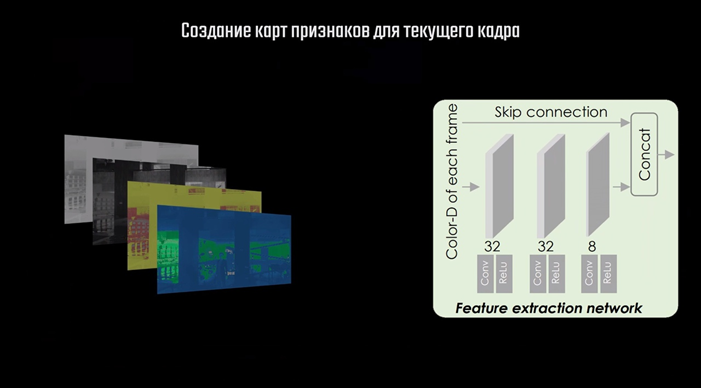


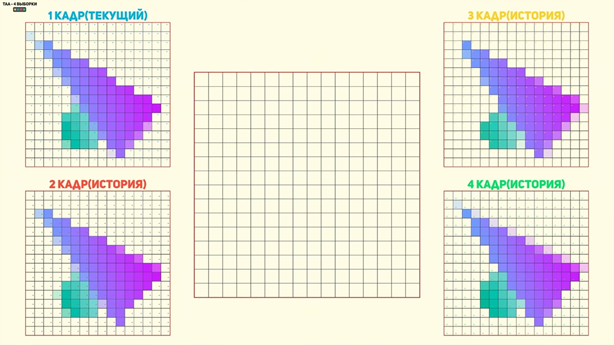
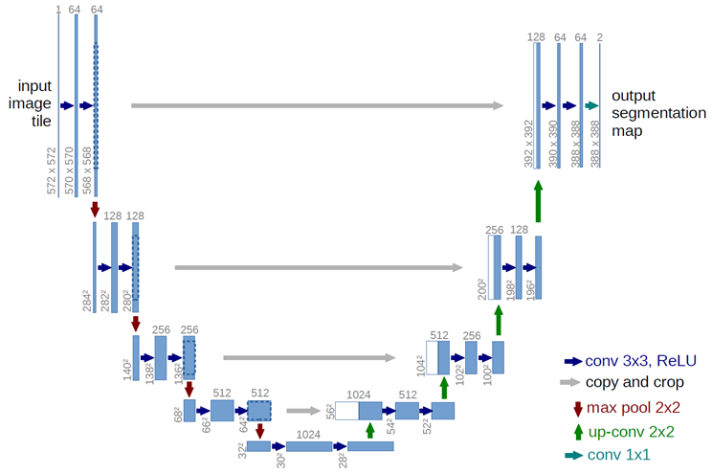









Лучшие комментарии
Каждый раз, когда вы слышите слово «нет», ваше тело думает, как можно ответить «да».
Это и есть нейронная сеть.
Например, если во время разговора собеседник говорит: «Я не могу прийти на встречу, потому что мне сейчас не хочется», вы мгновенно начинаете думать: «Ага, понятно, конечно, у него какие-то дела, но я все равно могу прийти».