Вы все наверняка слышали словосочетание «теорема Ферма». Теорема Ферма то, теорема Ферма се, некоторые даже считают, что именно ее и доказал Перельман. Это не так, он доказал гипотезу Пуанкаре, штука намного более сложная и интересная. Я вам про нее расскажу, как только ее пойму.
Revenons a nos moutons. В семнадцатом веке в Париже жил Пьер Ферма.
Математика для него была лишь хобби, работал он судьей. Приходя домой, он любил искать решения сложным теоремам, придумывать задачки, чтобы посложнее или просто читать математические книги. Одной из таких книг была «Арифметика» за авторством Диофанта Александрийского.
Трактат в тринадцати томах, посвященный общим методам решения уравнений. Книга была полна примеров, вопросов и недоказанных теорем. И Ферма, встречая их в тексте, всегда пытался их решить. Поскольку он обладал сильным умом, ему часто это удавалось, но просто так работать было скучно, а потому он оставлял на полях около теорем пометки в духе «я знаю, как это решить, но мне надо покормить кошку» или «я знаю, как это решить, но я должен вынести мусор». И вот он доходит до знаменитой теоремы Пифагора.
Она совсем простая, и подставлять числа туда легко и приятно. Ферма поднимает степени на переменных.
Становится сложнее, в уме так просто не подберешь. Ферма поднимает степень еще. Становится неясно, найдутся ли такие числа вообще? Он записывает на полях свою известную теорему.
Формулировка проста: не существует таких натуральных (целых, неотрицательных) чисел x, y, z и n, которые удовлетворяли бы этому условию. Неизвестно, доказал ли Ферма эту теорему. Но известно, что, подумав над ней, он пишет рядом «Я доказал этот поистине удивительный факт, но поля этой книги слишком узки для доказательства».
И тут он отбрасывает коньки.
Через тридцать лет его сын публикует переиздание «Арифметики», где все пометки Ферма-старшего включены в текст.
И математики всего мира начинают, одну за другой, доказывать теоремы, которые Ферма, если верить его пометкам, уже доказал. Год за годом, десятилетие за десятилетием, одна за другой, теоремы падают побежденными. Но только не наш сегодняшний герой. Это уравнение не просто не дается математикам, оно отвечает, становясь сложнее с каждым шагом, создавая новые проблемы на пути к доказательству.
Так продолжается столетиями, до самого двадцатого века. Где-то в шестидесятых, в Кембридже, десятилетний Эндрю Уайлс находит в библиотеке книгу «Последнее уравнение» Эрика Темпла Белла. Книга была целиком посвящена теореме Ферма, и маленький Эндрю, воодушевившись, решает, что именно он и должен решить ее. Разумеется, у него ничего не выходит. Но он не сдается. Он поступает в Кембридж, получает диплом, а затем и докторскую степень в математике. Теорема Ферма уже давно забыта, и Уайлс работает профессором математики в своей альма-матер.
И тут два японца, Шимура и Тонияма, формулируют гипотезу, внимание, Шимуры-Тониямы. Чудовищная вещь, надо полагать, только ее авторы до конца понимали суть. Но в какой-то момент времени было обнаружено, что теорема Ферма глубоко зашита в гипотезу, и если у кого-то получится доказать ее, то доказательство теоремы он получит совершенно бесплатно, в довесок. И Уайлс снова берется за дело, через тридцать с лишним лет. Он посвящает все свое свободное время доказательству гипотезы, но лишь потому, что это даст ему доказательство теоремы Ферма, его детской мечты. Эндрю Уайлс начинает пропускать собрания персонала, пропадать на работе. Доказательство съедает все его время.
И вот, после семи лет трудов, в 1993 году, доказательство готово. Математик дает серию из трех лекций, объясняя доказательство. В лекционном зале яблоку негде упасть, весь мир торжествует, Уайлс путешествует по свету, давая лекции, он теперь сэр Эндрю Уайлс, лауреат премии Шао.
Но теорема так просто не сдается. Во время проверки выясняется, что Уайлсом была допущена ошибка. Он берет несколько своих самых способных студентов и пытается исправить доказательство. И вот, через год упорных трудов, ошибка исправлена. Доказательство полностью верно, теорема доказана.
Победа.



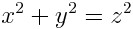
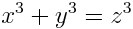
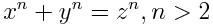











Лучшие комментарии
Сюда даже Войну и Мир можно поместить поделив его на части.
А то не ясно что за единицы и за нули. И вдруг это сложние по модулю два? Тогда плюс должен быть в кружочке.